Zadanie nr 5635534
Liczby 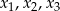 są rozwiązaniami równania
są rozwiązaniami równania 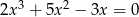 . Suma
. Suma 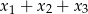 jest równa
jest równa
A) 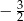 B)
B) 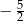 C)
C) 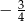 D)
D) 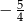
Rozwiązanie
Widać, że jednym z rozwiązań równania jest 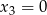 . Aby wyznaczyć pozostałe rozwiązania rozwiązujemy równanie
. Aby wyznaczyć pozostałe rozwiązania rozwiązujemy równanie
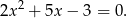
Sposób I
Liczymy
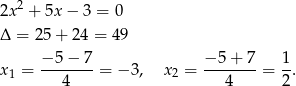
Zatem
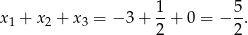
Sposób II
Korzystamy ze wzorów Viète’a dla równania kwadratowego.
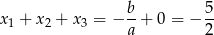
Sposób III
Korzystamy ze wzorów Viète’a dla równania stopnia 3
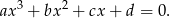
Mamy zatem
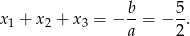
Odpowiedź: B

