/Szkoła średnia/Zadania testowe/Równania/Wielomianowe

Zadanie nr 6386064

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczba rzeczywistych rozwiązań równania 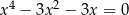4 2 x − 3x − 3x = 0 jest równa
A) 1 B) 2 C) 3 D) 4

Rozwiązanie

Jednym z pierwiastków jest oczywiście 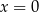x = 0 . Wystarczy więc zająć się równaniem

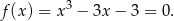
f(x ) = x3 − 3x − 3 = 0.

Liczymy pochodną lewej strony równania

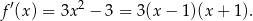
f′(x ) = 3x2 − 3 = 3(x − 1)(x+ 1).

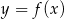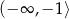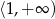Widać teraz, że funkcja y = f (x) rośnie w przedziałach (− ∞ ,− 1⟩ i ⟨1,+ ∞ ) oraz maleje w przedziale 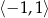⟨− 1,1⟩ . Ponadto,

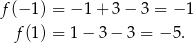
f(− 1) = − 1 + 3 − 3 = − 1 f(1) = 1 − 3 − 3 = − 5.

To pozwala naszkicować wykres funkcji 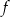f .

PIC

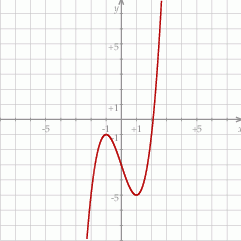
Z wykresu powinno być jasne, że równanie 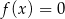f(x) = 0 ma jedno rozwiązanie. Wyjściowe równanie ma więc 2 rozwiązania.  
Odpowiedź: B

Wersja PDF