/Szkoła średnia/Zadania testowe/Równania/Wielomianowe/Stopnia 3

Zadanie nr 4274004

Ile różnych pierwiastków ma wielomian 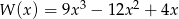3 2 W (x) = 9x − 1 2x + 4x ?
A) 0 B) 1 C) 2 D) 3

Wersja PDF

Rozwiązanie

Zauważmy, że

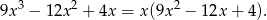
3 2 2 9x − 12x + 4x = x(9x − 12x + 4).

Zatem jednym z pierwiastków jest 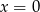x = 0 . Sprawdźmy teraz ile pierwiastków ma trójmian w nawiasie (liczymy 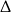Δ -ę).

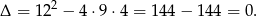
Δ = 122 − 4 ⋅9 ⋅4 = 144 − 14 4 = 0.

W takim razie trójmian ma jeden pierwiastek, a cały wielomian dwa.  
Odpowiedź: C

Wersja PDF