Zadanie nr 5047989
Dany jest wielomian 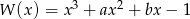 , gdzie
, gdzie  i
i 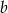 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Jeżeli równanie 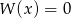 ma pierwiastek wymierny, to
ma pierwiastek wymierny, to 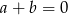 .
.
B) Jeżeli równanie 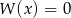 ma ujemny pierwiastek całkowity, to
ma ujemny pierwiastek całkowity, to 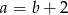 .
.
C) Równanie 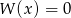 może nie mieć rozwiązań.
może nie mieć rozwiązań.
D) Równanie 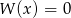 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
Rozwiązanie
Dane równanie nie musi mieć dwóch różnych pierwiastków, bo np. dla 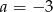 i
i 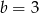 mamy
mamy
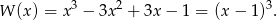
Z drugiej strony, przynajmniej jeden pierwiastek równanie ma zawsze, bo
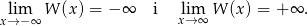
Jeżeli równanie ma pierwiastek wymierny 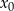 , to musi być on całkowity i musi to być dzielnik wyrazu wolnego, czyli
, to musi być on całkowity i musi to być dzielnik wyrazu wolnego, czyli 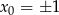 . Mamy zatem
. Mamy zatem
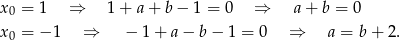
Odpowiedź: B

