Zadanie nr 7515590
Liczba niewymiernych pierwiastków równania 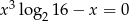 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Rozwiązanie
Ponieważ 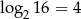 dane równanie możemy zapisać w postaci
dane równanie możemy zapisać w postaci
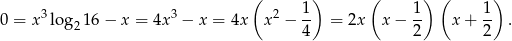
Zatem 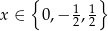 . Widać, że wszystkie pierwiastki są wymierne.
. Widać, że wszystkie pierwiastki są wymierne.
Odpowiedź: A
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Liczba niewymiernych pierwiastków równania 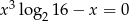 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Ponieważ 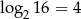 dane równanie możemy zapisać w postaci
dane równanie możemy zapisać w postaci
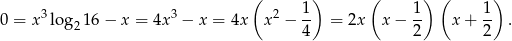
Zatem 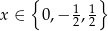 . Widać, że wszystkie pierwiastki są wymierne.
. Widać, że wszystkie pierwiastki są wymierne.
Odpowiedź: A
