/Szkoła średnia/Zadania testowe/Równania/Wielomianowe/Stopnia 4

Zadanie nr 6838348

Suma wszystkich pierwiastków wielomianu 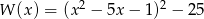2 2 W (x) = (x − 5x − 1) − 25 jest równa
A) 6 B) 9 C) 10 D) 11

Wersja PDF

Rozwiązanie

Rozwiązujemy równanie 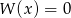W (x ) = 0 .

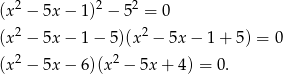
2 2 2 (x − 5x− 1) − 5 = 0 (x2 − 5x− 1− 5)(x2 − 5x − 1 + 5) = 0 2 2 (x − 5x− 6)(x − 5x + 4) = 0 .

Sposób I

Łatwo sprawdzić, że każde z równań kwadratowych w nawiasach ma dwa rozwiązania rzeczywiste. Na mocy wzorów Viète’a suma rozwiązań każdego z tych równań jest równa 5. Zatem suma wszystkich pierwiastków wielomianu 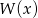W (x) jest równa 10.

Sposób II

Rozwiązujemy otrzymane równania kwadratowe.

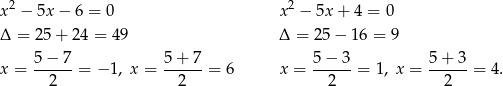
2 2 x − 5x− 6 = 0 x − 5x + 4 = 0 Δ = 25 + 2 4 = 49 Δ = 2 5− 16 = 9 x = 5-−-7-= − 1, x = 5-+-7-= 6 x = 5-−-3-= 1, x = 5-+-3-= 4. 2 2 2 2

Suma wszystkich pierwiastków wielomianu 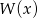W (x ) jest więc równa

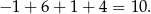
−1 + 6 + 1 + 4 = 10.

 
Odpowiedź: C

Wersja PDF