/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Czworokąt

Zadanie nr 4060885

Dodaj do ulubionych
Dodaj do rozwiązanych

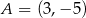Punkt A = (3,− 5) jest wierzchołkiem kwadratu 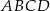ABCD , a punkt 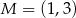M = (1,3) jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu 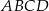ABCD jest równe
A) 68 B) 136 C) 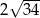2√ 34- D) √ --- 8 34

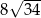
Rozwiązanie

Szkicujemy kwadrat.

PIC

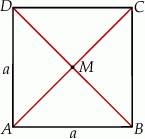
Punkt przecięcia się przekątnych dzieli każdą z nich na połowy, więc

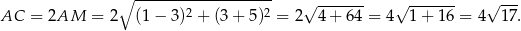
∘ ------------------- √ ------- √ ------- √ --- AC = 2AM = 2 (1− 3)2 + (3 + 5 )2 = 2 4+ 64 = 4 1 + 16 = 4 17.

Jeżeli teraz oznaczymy przez a długość boku kwadratu, to mamy

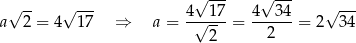
√ --- √ --- √ -- √ --- 4√-17- 4--34- √ --- a 2 = 4 17 ⇒ a = 2 = 2 = 2 34

Pole kwadratu jest więc równe

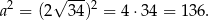
√ --- a 2 = (2 34)2 = 4 ⋅34 = 1 36.

 
Odpowiedź: B

Wersja PDF