/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Czworokąt

Zadanie nr 6274505

Dodaj do ulubionych
Dodaj do rozwiązanych

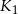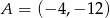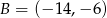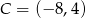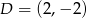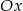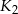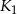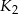Kwadrat K1 o wierzchołkach A = (− 4,− 12) , B = (− 14,− 6) , C = (− 8,4) i D = (2,− 2) przekształcono w symetrii względem osi Ox i otrzymano kwadrat K 2 . Odległość między środkami kwadratów K1 i K 2 jest równa
A) 4 B) 8 C) 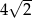√ -- 4 2 D) √ -- 8 2

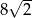
Rozwiązanie

Szkicujemy opisaną sytuację

PIC

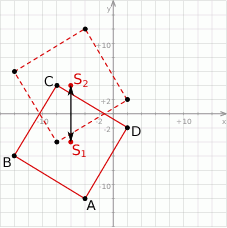
Środek 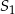S 1 pierwszego kwadratu to np. środek odcinka 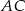AC , czyli

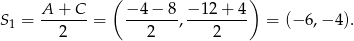
( ) S1 = A--+-C-= −-4−--8, −-12-+-4 = (− 6,− 4). 2 2 2

Punkt 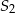S 2 będący odbiciem punktu 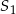S 1 względem osi 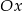Ox ma taką samą pierwszą współrzędną jak 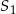S1 , a jego druga współrzędna różni się znakiem w stosunku do drugiej współrzędnej 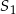S 1 . W takim razie 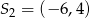S = (− 6 ,4 ) 2 i

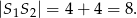
|S1S 2| = 4+ 4 = 8.

 
Odpowiedź: B

Wersja PDF