/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Czworokąt

Zadanie nr 7603308

Dodaj do ulubionych
Dodaj do rozwiązanych

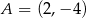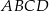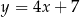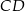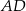Punkt A = (2,− 4) jest wierzchołkiem prostokąta ABCD . Prosta o równaniu y = 4x+ 7 zawiera bok CD . Bok AD zawiera się w prostej o równaniu
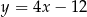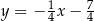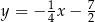A) y = 4x− 12 B) y = − 1x − 7 4 4 C) 1 7 y = − 4x − 2 D) y = 4x + 4

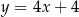
Rozwiązanie

Zaczynamy naturalnie od szkicowego rysunku.

PIC

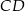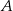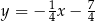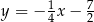Z rysunku widać, że musimy znaleźć równanie prostej prostopadłej do CD i przechodzącej przez punkt A . Z podanych prostych tylko y = − 14x− 74 i y = − 1x − 7 4 2 są prostopadłe do 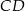CD . Łatwo sprawdzić (podstawiając współrzędne), że druga z tych prostych przechodzi przez punkt A .  
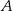Odpowiedź: C

Wersja PDF