Zadanie nr 8691697
Boki równoległoboku 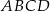 zwierają się w prostych o równaniach:
zwierają się w prostych o równaniach:
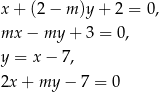
Zatem
A) 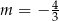 B)
B) 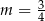 C)
C) 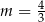 D)
D) 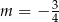
Rozwiązanie
Zauważmy, że równanie prostej 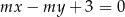 możemy zapisać w postaci
możemy zapisać w postaci
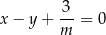
(dla 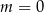 to równanie nie opisuje prostej), więc prosta ta jest równoległa do prostej
to równanie nie opisuje prostej), więc prosta ta jest równoległa do prostej 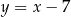 . To oznacza, że pozostałe dwie proste
. To oznacza, że pozostałe dwie proste
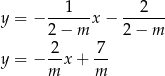
też muszą być równoległe. Zatem
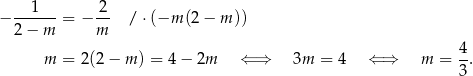
Odpowiedź: C

