/Szkoła średnia/Równania/Układy równań

Zadanie nr 1979442

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż układ równań 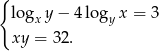{ logx y − 4 lo gyx = 3 xy = 32.

Rozwiązanie

Aby układ miał sens musi być 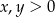x ,y > 0 i x ⁄= 1,y ⁄= 1 .

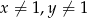Sposób I

Przekształćmy pierwsze równanie układu (zmieniamy podstawę na 2).

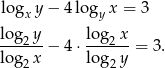
logxy − 4 logy x = 3 lo-g2y-− 4⋅ log-2x-= 3. lo g2x log 2y

Zanim zaczniemy to dalej przekształcać, zauważmy, że z drugiej równości mamy

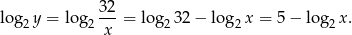
32 log2y = lo g2 x--= log2 32− lo g2x = 5− lo g2x.

Podstawmy teraz 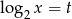log x = t 2 i poprzednia równość przyjmie postać

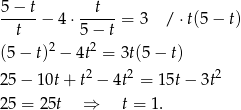
5−--t --t-- t − 4 ⋅5 − t = 3 / ⋅t(5− t) 2 2 (5 − t) − 4t = 3t(5− t) 2 5− 1 0t+ t2 − 4t2 = 15t − 3t2 2 5 = 25t ⇒ t = 1.

Zatem

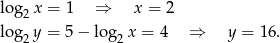
log2 x = 1 ⇒ x = 2 log y = 5− lo g x = 4 ⇒ y = 1 6. 2 2

Sposób II

Tym razem zmieńmy logarytmy w pierwszym równaniu na logarytmy o podstawie x .

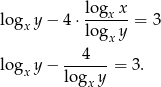
lo gxx logx y− 4⋅ lo-g-y-= 3 x log y− --4--- = 3. x log y x

Podstawiamy teraz 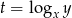t = log y x .

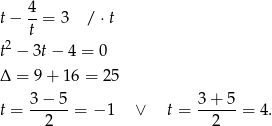
4- t − t = 3 / ⋅t 2 t − 3t− 4 = 0 Δ = 9 + 16 = 2 5 3− 5 3 + 5 t = -----= − 1 ∨ t = ------= 4. 2 2

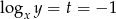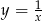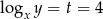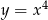Jeżeli logx y = t = − 1 to 1 y = x , co prowadzi do sprzeczności w drugim równaniu. Zatem lo gxy = t = 4 i y = x4 . Drugie równanie przyjmuje wtedy postać

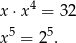
x⋅ x4 = 32 5 5 x = 2 .

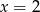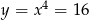Stąd x = 2 i y = x4 = 16 .  
Odpowiedź: (x,y ) = (2,16)

Wersja PDF