Zadanie nr 2952877
Określ liczbę rozwiązań układu równań 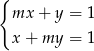 w zależności od wartości parametru
w zależności od wartości parametru 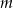 . Dla tych wartości
. Dla tych wartości 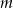 , dla których istnieją rozwiązania, rozwiąż ten układ.
, dla których istnieją rozwiązania, rozwiąż ten układ.
Rozwiązanie
Sposób I
Próbujemy rozwiązać podany układ. Na razie nie przejmujemy się parametrem – ważne jest tylko, żeby przez niego nie dzielić (bo może być 0). Odejmujemy od pierwszego równania drugie pomnożone przez 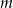 (żeby skrócić
(żeby skrócić  ).
).
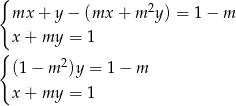
Widać teraz, że jeżeli 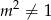 , to możemy jednoznacznie wyliczyć
, to możemy jednoznacznie wyliczyć  i
i 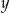
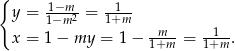
Jeżeli natomiast 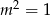 , to
, to 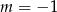 lub
lub 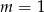 . Dla
. Dla 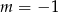 pierwsze równanie jest sprzeczne i układ nie ma rozwiązań. Dla
pierwsze równanie jest sprzeczne i układ nie ma rozwiązań. Dla 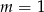 , pierwsze równanie jest spełnione przez dowolnego
, pierwsze równanie jest spełnione przez dowolnego 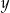 -ka, a z drugiego równania mamy
-ka, a z drugiego równania mamy 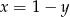 . Zatem układ spełnia dowolna para
. Zatem układ spełnia dowolna para 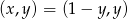 .
.
Sposób II
Korzystamy z metody wyznacznikowej. Liczymy wyznacznik główny układu
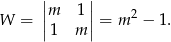
Jeżeli 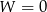 , czyli
, czyli 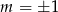 , to sprawdzamy ręcznie jak wygląda układ – podobnie jak w poprzednim podpunkcie. Jeżeli natomiast
, to sprawdzamy ręcznie jak wygląda układ – podobnie jak w poprzednim podpunkcie. Jeżeli natomiast 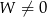 , to rozwiązania układu są równe
, to rozwiązania układu są równe
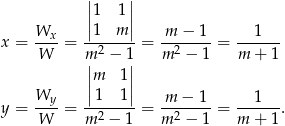
Odpowiedź: 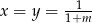 dla
dla 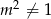 ;
; 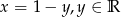 dla
dla 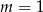 ; sprzeczny dla
; sprzeczny dla