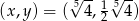/Szkoła średnia/Równania/Układy równań

Zadanie nr 3599198

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż układ równań 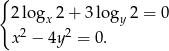{ 2logx 2+ 3logy 2 = 0 x2 − 4y2 = 0.

Rozwiązanie

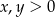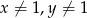Aby podany układ miał sens, musi być x,y > 0 i x ⁄= 1,y ⁄= 1 . Przekształćmy pierwsze równanie układu (zmieniamy podstawę logarytmu na 2).

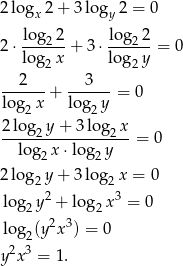
2 logx 2+ 3logy 2 = 0 log 2 log 2 2 ⋅----2- + 3 ⋅---2-- = 0 log 2x log2 y --2--- --3--- lo g x + lo g y = 0 2 2 2log2-y+--3log2-x-= 0 lo g2x ⋅log2 y 2 log2y + 3 log2 x = 0 lo g y 2 + log x3 = 0 2 2 3 2 lo g2(y x ) = 0 2 3 y x = 1.

Z drugiego równania mamy 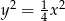2 1 2 y = 4 x , co daje nam równanie

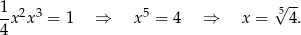
1 √5-- --x2x3 = 1 ⇒ x5 = 4 ⇒ x = 4. 4

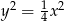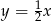Z równości 2 1 2 y = 4 x mamy 1 y = 2x (bo obie liczby są dodatnie). Zatem

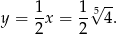
1 1√5-- y = -x = -- 4. 2 2

 
Odpowiedź: 5√ --1√5-- (x ,y ) = ( 4,2 4 )

Wersja PDF