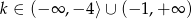Zadanie nr 3794267
Dla jakich wartości parametru 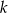 wśród rozwiązań układu równań:
wśród rozwiązań układu równań:
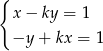
jest para liczb 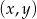 spełniających warunek:
spełniających warunek: 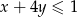 ?
?
Rozwiązanie
Sposób I
Spróbujmy rozwiązać ten układ równań. Od pierwszego równania odejmujemy drugie pomnożone przez 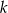 (żeby skrócić
(żeby skrócić 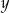 ).
).
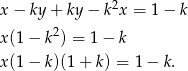
Jeżeli 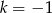 to powyższa równość jest sprzeczna. Jeżeli
to powyższa równość jest sprzeczna. Jeżeli 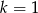 to
to  jest dowolne, a
jest dowolne, a 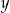 wyraża się wzorem
wyraża się wzorem
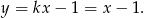
Mamy wtedy
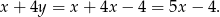
Z pewnością można więc znaleźć  , dla którego
, dla którego 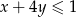 (np.
(np. 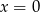 ).
).
Pozostał nam przypadek 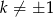 . Mamy wtedy
. Mamy wtedy 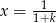 oraz
oraz
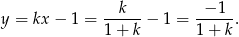
Pozostało rozwiązać nierówność
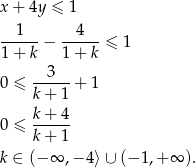
Uwzględniając wcześniej rozważone przypadki mamy 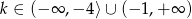 .
.
Sposób II
Tym razem zastosujemy metodę wyznacznikową. Liczymy wyznaczniki.
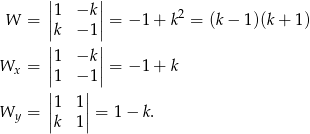
Widać teraz, że jeżeli 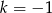 to układ jest sprzeczny (bo
to układ jest sprzeczny (bo 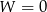 i
i 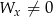 ).
).
Jeżeli 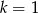 to układ jest nieoznaczony i równoważny równaniu
to układ jest nieoznaczony i równoważny równaniu 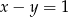 . Oczywiście znajdziemy wśród liczb spełniających to równanie parę spełniającą dodatkowo
. Oczywiście znajdziemy wśród liczb spełniających to równanie parę spełniającą dodatkowo 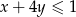 (wystarczy np., że
(wystarczy np., że 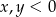 , np.
, np. 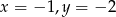 ).
).
Pozostał do rozpatrzenia przypadek 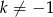 i
i 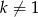 . Układ ma wtedy dokładnie jedno rozwiązanie
. Układ ma wtedy dokładnie jedno rozwiązanie
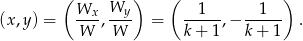
Pozostało rozwiązać nierówność
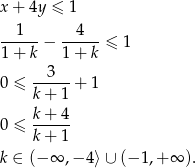
Uwzględniając wcześniej rozważone przypadki mamy 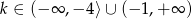 .
.
Odpowiedź: