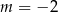Zadanie nr 3857198

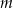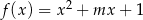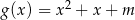Dla jakiej wartości parametru funkcje 2 f(x ) = x + mx + 1 i 2 g(x) = x + x + m mają wspólne miejsce zerowe?

Rozwiązanie

Jeżeli jest wspólnym miejscem zerowym podanych funkcji, to spełnia układ równań

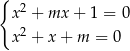
{ x 2 + mx + 1 = 0 x 2 + x + m = 0

Odejmujemy od pierwszego równania drugie i mamy

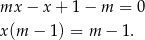
mx − x + 1− m = 0 x(m − 1) = m − 1.

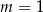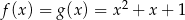Jeżeli m = 1 , to f(x) = g (x) = x2 + x + 1 i żadna z tych funkcji nie ma miejsc zerowych. Możemy więc założyć, że 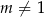m ⁄= 1 i wtedy powyższa równość oznacza, że wspólnym miejscem zerowym funkcj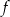i i 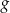musi być 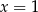x = 1 . Sprawdzamy (np. wstawiając 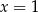x = 1 do układu równań), że tak jest tylko dla m = − 2 .
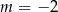Odpowiedź: