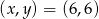/Szkoła średnia/Równania/Układy równań

Zadanie nr 9018447

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż układ równań 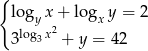{ logy x + logx y = 2 3log3x2 + y = 42 .

Rozwiązanie

Podany układ ma sens dla 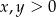x ,y > 0 i x ⁄= 1 , y ⁄= 1 .

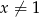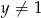Drugie równanie możemy przepisać jako

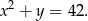
x2 + y = 42 .

Przekształcamy teraz pierwsze.

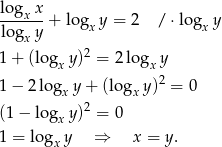
logx-x + log y = 2 / ⋅log y logx y x x 2 1+ (lo gxy) = 2logx y 1− 2log y+ (lo g y )2 = 0 x x (1− lo gxy)2 = 0 1 = log y ⇒ x = y . x

Wracamy teraz do drugiego równania

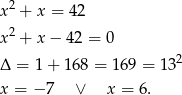
x 2 + x = 42 x 2 + x − 4 2 = 0 2 Δ = 1 + 168 = 169 = 13 x = − 7 ∨ x = 6 .

Oczywiście ujemne rozwiązanie odrzucamy i mamy 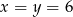x = y = 6 .  
Odpowiedź: (x,y ) = (6,6)

Wersja PDF