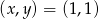Zadanie nr 9318654
Rozwiąż układ równań 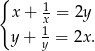
Rozwiązanie
Z pierwszego równania mamy
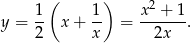
Podstawiamy to wyrażenie do drugiego równania.
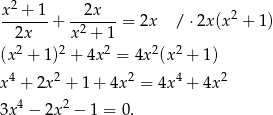
Otrzymaliśmy równanie dwukwadratowe, więc podstawiamy 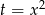 .
.
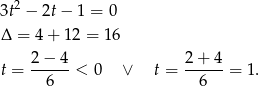
Ujemne rozwiązanie odrzucamy (bo 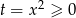 ) i mamy
) i mamy 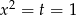 . Zatem
. Zatem 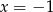 lub
lub 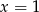 . Mamy wtedy odpowiednio
. Mamy wtedy odpowiednio 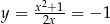 i
i 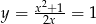 .
.
Odpowiedź: 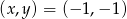 lub
lub