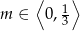Zadanie nr 9702863
Dla jakich wartości parametru 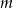 rozwiązaniem układu równań
rozwiązaniem układu równań 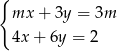 jest para liczb nieujemnych?
jest para liczb nieujemnych?
Rozwiązanie
Sposób I
Nie przejmujemy się parametrem i rozwiązujemy podany układ równań. Odejmujemy od drugiego równania pierwsze pomnożone przez 2 (żeby skrócić 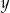 ).
).
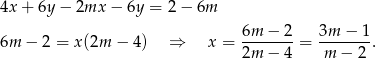
Z drugiego równania układy obliczamy teraz 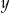 .
.
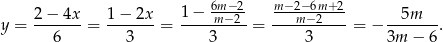
Oczywiście ten rachunek ma sens tylko jeżeli 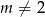 .
.
Pozostało teraz rozwiązać nierówności
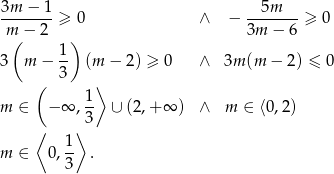
Sposób II
Podany układ wygodnie jest rozwiązać metodą wyznacznikową
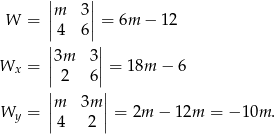
Stąd

Dalej rozwiązujemy jak w poprzednim sposobie.
Odpowiedź: