Zadanie nr 6435201
Dany jest kwadrat o przekątnej 4. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 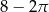 B)
B) 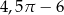 C)
C) 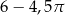 D)
D) 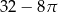
Rozwiązanie
Zaczynamy od rysunku
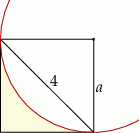
Liczymy długość boku kwadratu
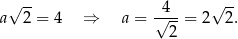
Obliczamy pole kwadratu
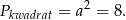
Obliczamy pole koła
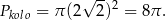
Pole części wspólnej koła i kwadratu stanowi 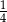 pola całego koła. Zatem szukane pole zakreskowanej części jest równe
pola całego koła. Zatem szukane pole zakreskowanej części jest równe
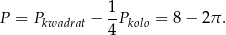
Odpowiedź: A

