/Szkoła średnia/Zadania testowe/Zadania z treścią/Własności liczb

Zadanie nr 4875617

Suma wszystkich liczb dwucyfrowych, które przy dzieleniu przez 4 dają resztę 3 jest równa
A) 1166 B) 1265 C) 1320 D) 1210

Wersja PDF

Rozwiązanie

Liczby dwucyfrowe dające resztę 3 przy dzieleniu przez 4 to

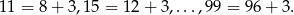
11 = 8 + 3,15 = 12+ 3,...,99 = 9 6+ 3 .

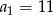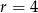Tworzą one ciąg arytmetyczny, w którym a1 = 1 1 i r = 4 . Sprawdźmy, którym wyrazem tego ciągu jest liczba 99.

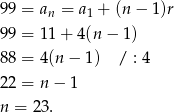
99 = an = a1 + (n− 1)r 99 = 1 1+ 4(n− 1) 88 = 4 (n− 1) / : 4 22 = n − 1 n = 23.

Korzystając ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego mamy

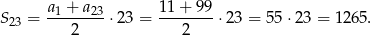
S 23 = a1 +-a23⋅ 23 = 11-+-9-9⋅2 3 = 55 ⋅23 = 12 65. 2 2

 
Odpowiedź: B

Wersja PDF