Zadanie nr 5782909
Pięć osób: Arek, Marta, Agnieszka, Edyta i Piotrek wybrało się do kina. Na ile sposobów mogą te osoby usiąść w jednym rzędzie na pięciu kolejnych miejscach tak, żeby Agnieszkę i Piotrka rozdzielała jedna osoba?
A) 48 B) 36 C) 24 D) 12
Rozwiązanie
Wyobraźmy sobie pięć kolejnych miejsc w jednym rzędzie

Agnieszkę i Piotrka musi rozdzielać jedna osoba, więc licząc od lewej mogą usiąść na pierwszym i trzecim, drugim i czwartym lub trzecim i piątym miejscu. Musimy jeszcze pamiętać o tym, że można zamienić ich miejscami, więc możliwości usadzenia Agnieszki i Piotrka jest
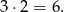
Pozostałe osoby możemy posadzić w dowolny sposób, więc jest
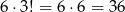
możliwości.
Odpowiedź: B

