/Szkoła średnia/Funkcje - wykresy/Sklejana z kilku funkcji

Zadanie nr 1993770

Dodaj do ulubionych
Dodaj do rozwiązanych

Naszkicuj wykres funkcji

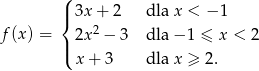
( |{ 3x + 2 dla x < − 1 f (x ) = 2x 2 − 3 dla − 1 ≤ x < 2 |( x + 3 dla x ≥ 2.

Odczytaj z wykresu maksymalne przedziały monotoniczności funkcji 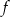f .

PIC

Rozwiązanie

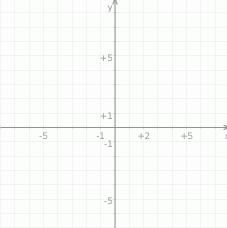
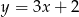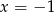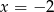Wykresem y = 3x + 2 jest prosta, aby ją naszkicować podstawiamy np. x = − 1 i x = − 2 . Oczywiście rysujemy ją tylko na lewo od x = − 1 .

PIC

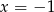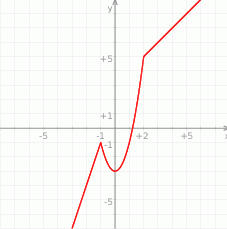
Potem szkicujemy fragment paraboli 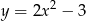y = 2x2 − 3 , która jest parabolą 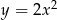y = 2x2 przesuniętą o 3 jednostki w dół. Żeby wiedzieć gdzie mamy zaznaczyć jej końce, podstawiamy do wzoru 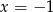x = − 1 oraz x = 2 .

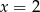Na koniec rysujemy fragment prostej 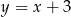y = x + 3 , która jest prostą 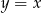y = x przesuniętą o 3 jednostki w górę.

W wykresu bez trudu odczytujemy, że funkcja jest rosnąca na przedziałach 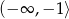(− ∞ ,− 1⟩ oraz na 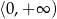⟨0,+ ∞ ) . Ponadto jest malejąca na przedziale ⟨− 1,0⟩ .  
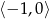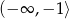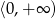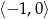Odpowiedź: Rosnąca na (− ∞ ,− 1⟩ i na ⟨0,+ ∞ ) . Malejąca na ⟨− 1,0⟩ .

Wersja PDF