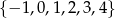/Szkoła średnia/Funkcje - wykresy/Sklejana z kilku funkcji

Zadanie nr 4172780

Funkcja f określona jest wzorem

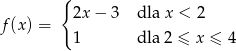
{ f(x) = 2x − 3 dla x < 2 1 dla 2 ≤ x ≤ 4
  • Uzupełnij tabelę:
    x -33 
    f(x)   0
  • Narysuj wykres funkcji f(x ) .
  • Podaj liczby całkowite x , spełniające nierówność f(x) ≥ − 6 .
Wersja PDF

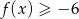Rozwiązanie

  • Liczymy
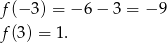
    f (− 3 ) = − 6− 3 = − 9 f (3 ) = 1.

    Ponadto widać, że wartość 0 może przyjmować tylko pierwszy wzór oraz

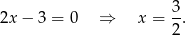
    3 2x − 3 = 0 ⇒ x = --. 2

    Teraz uzupełniamy tabelkę.

    x -33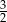3 2
    f(x)-91 0
  • Wykres będzie składał się z dwóch kawałków prostych (odcinka i półprostej).
    PIC
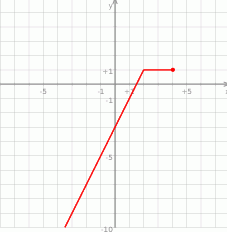
  • Możemy te liczby odczytać z wykresu, ale możemy też wyliczyć. Oczywiście nierówność ta będzie spełniona dla liczb z przedziału 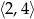⟨2,4⟩ . Zobaczmy jeszcze jakie liczby mniejsze od 2 ją spełniają.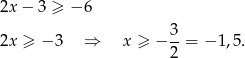
    2x − 3 ≥ − 6 3 2x ≥ − 3 ⇒ x ≥ − 2-= − 1,5.

    Daje to nam dodatkowo liczby {− 1,0,1} .  
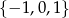    Odpowiedź: {− 1,0,1,2,3 ,4 }

Wersja PDF