Zestaw użytkownika nr 1288_3233

powtórka rozszerzenie

Zadanie 1
(4 pkt)

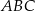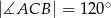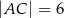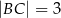W trójkącie ABC dane są kąt ∘ |∡ACB | = 12 0 , |AC | = 6 i |BC | = 3 . Dwusieczna kąta 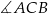∡ACB przecina bok 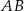AB w punkcie D .

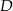  • Oblicz długość odcinka CD .
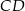  • Jaki jest związek miedzy długościami promieni: okręgu opisanego na trójkącie 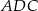ADC i okręgu opisanego na trójkącie 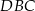DBC ? Odpowiedź uzasadnij.
Zadanie 2
(4 pkt)

Oblicz wartość wyrażenia 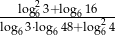log2 3+ log 16 log-36⋅log-486+log2-4 6 6 6 .

Zadanie 3
(4 pkt)

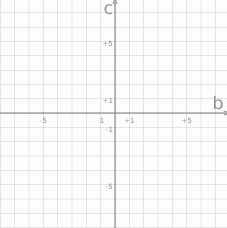
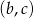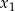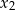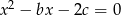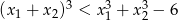W prostokątnym układzie współrzędnych narysuj zbiór tych wszystkich punktów o współrzędnych (b,c) , dla których różne pierwiastki x1 i x2 równania x 2 − bx − 2c = 0 spełniają warunek (x1 + x2)3 < x31 + x32 − 6 .

PIC

Zadanie 4
(4 pkt)

Ciąg 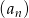(an) , gdzie 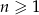n ≥ 1 dany jest wzorem rekurencyjnym

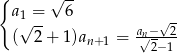
{ √ -- a√1 =- 6 √- ( 2+ 1 )an+1 = an√−--2 2− 1
  • Oblicz sumę 21 początkowych wyrazów tego ciągu.
  • Wyznacz wszystkie liczby naturalne n , dla których spełniona jest nierówność
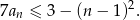
    2 7an ≤ 3 − (n − 1 ) .
Zadanie 5
(5 pkt)

Uzasadnij, że funkcja 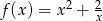2 2 f (x) = x + x przyjmuje dla dodatnich argumentów wartości nie mniejsze niż 3.

Zadanie 6
(5 pkt)

Ze zbioru 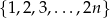{1,2,3,...,2n } , gdzie 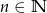n ∈ N , losujemy jednocześnie trzy liczby. Ile mamy możliwości wylosowania takich trzech liczb, których suma jest nieparzysta?

Zadanie 7
(3 pkt)

Wykaż, że dla każdej liczby rzeczywistej x prawdziwa jest nierówność:

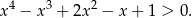
4 3 2 x − x + 2x − x + 1 > 0 .
Zadanie 8
(3 pkt)

Właściciel kiosku notował liczbę biletów komunikacji miejskiej sprzedanych w kolejnych godzinach. Wyniki obserwacji zapisał w tabeli.

Czas obserwacji Liczba biletów
5:00–6:00 2
6:00–7:00 3
7:00–8:00 9
8:00–9:00 8
9:00–10:00 6
10:00–11:00 4
11:00–12:00 3
12:00–13:00 3
13:00–14:00 3
14:00–15:00 5
15:00–16:00 8
16:00–17:00 6
  • Oblicz średnią liczbę biletów sprzedawanych w ciągu 1 godziny.
  • Wynikiem „typowym” nazywamy wynik, który różni się od średniej o mniej niż jedno odchylenie standardowe. Podaj wszystkie godziny, w których liczba sprzedanych biletów nie była „typowa”.
Zadanie 9
(5 pkt)

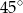Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa a . Kąt między krawędzią boczną i krawędzią podstawy ma miarę 4 5∘ . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.

Zadanie 10
(5 pkt)

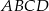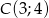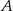W prostokącie ABCD dany jest wierzchołek C (3;4) oraz −→ AB = [4;3] . Znajdź równania przekątnych wiedząc, że wierzchołek A należy do prostej x − y = 5 .

Zadanie 11
(4 pkt)

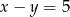Suma długości dwóch boków trójkąta jest równa 12cm, a kąt między tymi bokami ma miarę 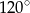1 20∘ . Oblicz jakie powinny być długości boków tego trójkąta aby jego pole było największe.

Zadanie 12
(4 pkt)

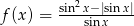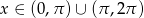Dana jest funkcja f określona wzorem sin2x−|sinx|- f(x) = sin x dla x ∈ (0,π) ∪ (π ,2 π) .

  • Naszkicuj wykres funkcji f .
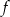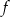  • Wyznacz miejsca zerowe funkcji f .
Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze