Zestaw użytkownika nr 2062_2812
Zestaw użytkownika
nr 2062_2812
Wiedząc, że  jest kątem ostrym oraz
jest kątem ostrym oraz 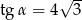 oblicz wartość wyrażenia
oblicz wartość wyrażenia 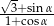 .
.
Znajdź najmniejszą i największą wartość funkcji 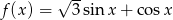 w przedziale
w przedziale 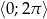 .
.
Wykaż, że jeżeli 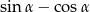 jest liczbą wymierną to wymierna jest również liczba
jest liczbą wymierną to wymierna jest również liczba 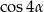 .
.
Wyznacz 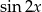 i
i 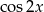 jeśli wiadomo że
jeśli wiadomo że 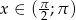 i
i 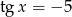 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 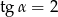 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 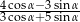 .
.
- Sprawdź, czy równość
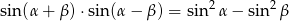
jest tożsamością trygonometryczną.
- Udowodnij, że jeżeli
 i
i 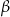 są dwoma kątami trójkąta i
są dwoma kątami trójkąta i 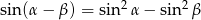 , to trójkąt ten jest trójkątem prostokątnym lub równoramiennym.
, to trójkąt ten jest trójkątem prostokątnym lub równoramiennym.
Wyznacz zbiór wartości funkcji 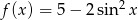 dla
dla 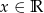 .
.
Wyznacz okres podstawowy funkcji 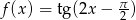 .
.
Wiedząc, że 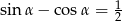 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 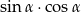 .
.
Wykaż, że nie istnieje kąt ostry  taki, że
taki, że 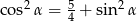 .
.
Dana jest funkcja 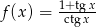 dla
dla 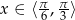 .
.
- Rozwiąż równanie
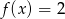 .
. - Wyznacz najmniejszą wartość funkcji
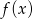 .
.
Wykaż, że wyrażenie 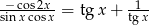 nie jest tożsamością.
nie jest tożsamością.
Wyznacz najmniejszą wartość funkcji 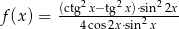 .
.
Uzasadnij, że liczba 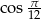 jest niewymierna.
jest niewymierna.
Wyznacz zbiór wartości funkcji: 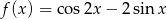 , gdzie
, gdzie 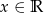 .
.
Kąt  jest kątem ostrym. Wiedząc, że
jest kątem ostrym. Wiedząc, że 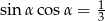 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 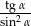 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 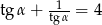 , oblicz
, oblicz 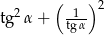 .
.
Wiedząc, że 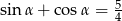 , oblicz
, oblicz 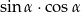 .
.
Wyznacz zbiór wartości funkcji
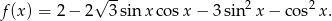
Oblicz 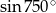 .
.
Wykaż, że jeśli 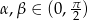 ,
, 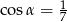 i
i 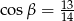 , to
, to 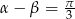 .
.
Wykaż, że nie istnieje kąt  , dla którego spełniona jest równość
, dla którego spełniona jest równość 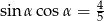 .
.
Dana jest funkcja 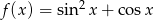 dla
dla 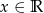 .
.
- Rozwiąż równanie
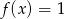 w przedziale
w przedziale 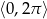 .
. - Wyznacz największą wartość funkcji
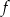 .
.
Sprawdź, czy prawdziwa jest następująca tożsamość 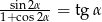 . Podaj konieczne założenia.
. Podaj konieczne założenia.
Kąta  jest ostry oraz
jest ostry oraz 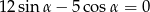 . Oblicz
. Oblicz 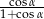 .
.
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to 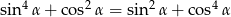 .
.
Oblicz wartość wyrażenia 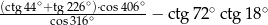 .
.

