Zestaw użytkownika nr 2681_6183
sprawdzian maturalny 1. semestr
Wykaż, że jeżeli 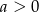 i
i 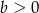 oraz
oraz 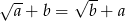 to
to 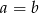 lub
lub 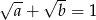 .
.
Uzasadnij, że jeśli 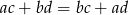 to
to 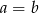 lub
lub 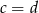 .
.
Oblicz wartość wyrażenia 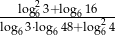 .
.
Funkcja 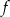 dana jest wzorem
dana jest wzorem
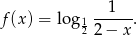
Określ dziedzinę funkcji 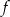 i naszkicuj jej wykres w przedziale
i naszkicuj jej wykres w przedziale 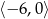 .
.
Wykaż, że wyrażenie 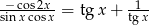 nie jest tożsamością.
nie jest tożsamością.
Wykaż, że nie istnieje kąt  , dla którego spełniona jest równość
, dla którego spełniona jest równość 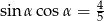 .
.
Sinus pewnego kąta ostrego  , liczba
, liczba  oraz cosinus tego samego kąta
oraz cosinus tego samego kąta  tworzą w podanej kolejności ciąg geometryczny. Oblicz sumę
tworzą w podanej kolejności ciąg geometryczny. Oblicz sumę 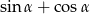 .
.
Ciąg 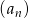 określony jest wzorem
określony jest wzorem 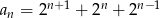 .
.
- Oblicz pierwszy i trzeci wyraz tego ciągu.
- Uzasadnij, korzystając z definicji ciągu geometrycznego, że ciąg
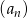 jest geometryczny.
jest geometryczny.
Dla jakich wartości parametru  równanie
równanie 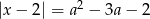 ma dwa pierwiastki różnych znaków?
ma dwa pierwiastki różnych znaków?
Różnymi pierwiastkami równania kwadratowego 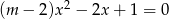 są liczby
są liczby 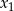 oraz
oraz 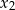 . Narysuj wykres funkcji
. Narysuj wykres funkcji 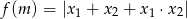 .
.
Zbadaj dla jakich wartości parametru 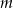 punkt przecięcia się prostych
punkt przecięcia się prostych 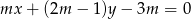 i
i 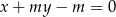 należy do prostokąta o wierzchołkach
należy do prostokąta o wierzchołkach 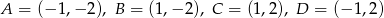 ?
?
Za pomocą rachunku wektorowego pokazać, że środki boków dowolnego czworokąta tworzą wierzchołki równoległoboku.
Na płaszczyźnie dane są punkty 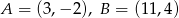 . Na prostej o równaniu
. Na prostej o równaniu 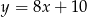 znajdź punkt
znajdź punkt 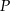 , dla którego suma
, dla którego suma 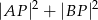 jest najmniejsza.
jest najmniejsza.
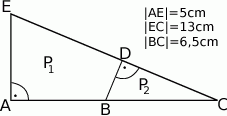
Dany jest czworokąt o kolejnych bokach długości 3,4,5 oraz kącie  między bokami długości 3 i 4 takim, że
między bokami długości 3 i 4 takim, że 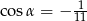 . Wyznacz długość czwartego boku, jeśli wiadomo, że na czworokącie można opisać okrąg.
. Wyznacz długość czwartego boku, jeśli wiadomo, że na czworokącie można opisać okrąg.
Wyznacz liczbę  , wiedząc że
, wiedząc że 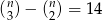 .
.
Uzasadnij, że jeśli liczby rzeczywiste 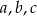 spełniają nierówności
spełniają nierówności 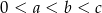 , to
, to
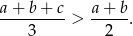
Antek zatrudnił się przy zbiórce truskawek. Każdego dnia zbiera taką samą liczbę kilogramów owoców i w sumie uzbierał 96 kilogramów. Gdyby każdego dnia zbierał o 4 kilogramy więcej, to tę samą ilość owoców uzbierałby w czasie krótszym o cztery dni. Oblicz, ile kilogramów owoców zbierał Antek każdego dnia i w ciągu ilu dni je zebrał.
Dziadek założył w banku trzyletnią lokatę pieniężną o stałej rocznej stopie procentowej równej 5% (już po uwzględnieniu podatków i prowizji). Odsetki są kapitalizowane po każdym roku trwania lokaty. Całość środków, otrzymanych z banku po zlikwidowaniu lokaty, dziadek podzielił równo pomiędzy dziewięcioro wnucząt tak, że każde z dzieci otrzymało 1029 zł. Oblicz początkową kwotę lokaty.
Motorówka płynęła z prądem rzeki od przystani  do przystani
do przystani  przez 40 minut, a wracała 56 minut. Oblicz prędkość motorówki i prędkość prądu rzeki, jeżeli przystanie
przez 40 minut, a wracała 56 minut. Oblicz prędkość motorówki i prędkość prądu rzeki, jeżeli przystanie 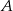 i
i 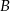 są odległe o 14km.
są odległe o 14km.
Państwo Nowakowie przeznaczyli 26000 zł na zakup działki. Do jednej z ofert dołączono rysunek w skali 1:1000 dwóch przylegających do siebie działek. Jeden metr kwadratowy gruntu w tej ofercie kosztuje 35 zł. Oblicz, czy przeznaczona przez państwa Nowaków kwota wystarczy na zakup działki 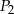 .
.