Zestaw użytkownika nr 2708_1356

Zestaw użytkownika
nr 2708_1356

Zadanie 1

Dane są funkcje 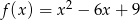2 f(x) = x − 6x+ 9 i g(x) = x + 7 .

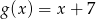  • Znajdź te argumenty, dla których zarówno funkcja 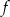f , jak i funkcja 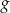g przyjmują wartości dodatnie.
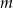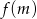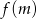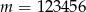  • Uzasadnij, że dla każdej liczby całkowitej m liczba f(m ) jest kwadratem liczby całkowitej. Kwadratem jakiej liczby naturalnej jest f(m ) , jeżeli m = 1234 56 ?
Zadanie 2

Rozwiąż równanie 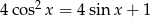2 4co s x = 4 sin x + 1 w przedziale ⟨0,2π ⟩ .

Zadanie 3

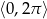Podstawą graniastosłupa prawidłowego jest trójkąt, w którym długość wysokości wynosi 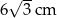√ -- 6 3cm . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt o mierze 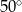50∘ . Oblicz pole powierzchni całkowitej i objętość graniastosłupa. Wynik podaj z dokładnością do 1cm.

Zadanie 4

Danych jest osiem kul z numerami od 1 do 8, oraz dziesięć szuflad z numerami od 1 do 10. Rozmieszczamy w dowolny sposób kule w szufladach. Oblicz prawdopodobieństwa następujących zdarzeń:

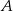  • A – wszystkie kule znajdą się w szufladach z numerami parzystymi.
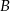  • B – dokładnie dwie szuflady pozostaną puste.
Zadanie 5

Spośród wyrazów skończonego ciągu arytmetycznego 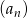(an) danego wzorem 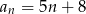an = 5n + 8 , gdzie 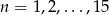n = 1,2,...,15 wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.

Zadanie 6

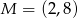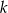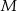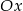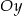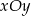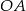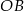Dany jest punkt M = (2 ,8 ) . Wyznacz równanie takiej prostej k , do której należy punkt M , że na ujemnej półosi Ox i dodatniej półosi Oy układu xOy prosta ta wyznacza odcinki OA i OB , których suma długości jest równa 6. Oblicz obwód trójkąta AOB .

Zadanie 7

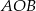Rozwiąż nierówność 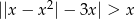2 ||x− x |− 3x | > x .

Zadanie 8

Suma dwóch liczb równa jest 6. Znajdź te liczby, jeśli wiadomo, że suma podwojonego kwadratu jednej z nich i kwadratu drugiej jest najmniejsza z możliwych.

Zadanie 9

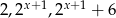Znajdź x , dla którego liczby x+ 1 x+1 2,2 ,2 + 6 w podanej kolejności tworzą ciąg arytmetyczny.

Zadanie 10

Podstawą ostrosłupa 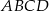ABCD jest trójkąt 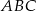ABC . Krawędź 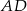AD jest wysokością ostrosłupa (zobacz rysunek).

PIC

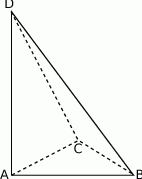
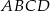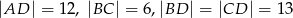Oblicz objętość ostrosłupa ABCD , jeśli wiadomo, że |AD | = 12, |BC | = 6,|BD | = |CD | = 13 .

Zadanie 11

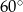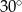W trapezie kąty przy dłuższej podstawie to ∘ 60 i ∘ 30 , a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.

Zadanie 12

Podstawą graniastosłupa jest trójkąt prostokątny równoramienny o ramieniu długości 9. Kąt między przekątną największej ściany bocznej i wysokością graniastosłupa jest równy 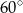60∘ . Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.

Zadanie 13

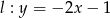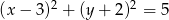Wykaż, że prosta l : y = − 2x − 1 jest styczna do okręgu 2 2 (x − 3) + (y + 2) = 5 .

Zadanie 14

Punkt 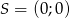S = (0 ;0) jest środkiem boku 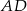AD równoległoboku 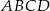ABCD . Wiadomo też, że −→ AB = [4;3] oraz −→ BC = [6;2] . Wyznacz wierzchołki tego równoległoboku.

Zadanie 15

Wyznacz wszystkie rozwiązania równania 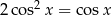2 2co s x = co sx należące do przedziału ⟨0,2π ⟩ .

Zadanie 16

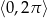Mariusz Czerkawski i Jimmy O’Brien w jednym sezonie NHL zdobyli w sumie 100 bramek. Kluby obu zawodników za każdą zdobytą bramkę wypłacały hokeistom z góry ustaloną premię. Po sezonie okazało się, że obaj zawodnicy otrzymali za strzelone bramki równe kwoty. Gdyby Czerkawski zdobył tyle bramek ile O’Brien, to otrzymałby 72000$, zaś gdyby drugi strzelił tyle bramek ile pierwszy, to otrzymałby 32000$. Oblicz, ile bramek zdobył każdy z nich i jaka była wysokość premii w obu klubach za strzelenie bramki.

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze