Zestaw użytkownika nr 3093_5495
FUNKCJA HOMOGRAFICZNA
Funkcja 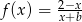 przyjmuje wartości ujemne wtedy i tylko wtedy gdy
przyjmuje wartości ujemne wtedy i tylko wtedy gdy 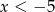 lub
lub 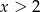 .
.
- Oblicz
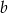 .
. - Napisz wzór funkcji
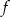 w postaci kanonicznej.
w postaci kanonicznej. - Wyznacz zbiór tych argumentów, dla których funkcja
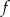 osiąga wartości nie większe niż funkcja
osiąga wartości nie większe niż funkcja 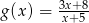 .
.
Funkcja homograficzna 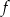 jest monotoniczna w przedziałach
jest monotoniczna w przedziałach 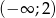 i
i 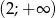 . Zbiór
. Zbiór 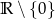 jest zbiorem wartości tej funkcji, a wartość 1 funkcja przyjmuje dla argumentu 6.
jest zbiorem wartości tej funkcji, a wartość 1 funkcja przyjmuje dla argumentu 6.
- Znajdź wzór funkcji
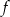 .
. - Naszkicuj wykres funkcji
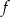 .
. - Uzasadnij, że funkcja
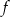 nie jest monotoniczna w zbiorze
nie jest monotoniczna w zbiorze 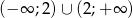 .
.
W prostokątnym układzie współrzędnych zaznacz zbiór tych wszystkich punktów płaszczyzny o współrzędnych 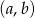 , dla których funkcja
, dla których funkcja 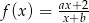 jest funkcją homograficzną, malejącą w każdym z przedziałów:
jest funkcją homograficzną, malejącą w każdym z przedziałów: 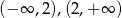 .
.
Funkcja homograficzna jest określona wzorem 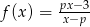 gdzie
gdzie 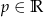 i
i 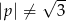 .
.
- Dla
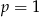 zapisz wzór funkcji w postaci
zapisz wzór funkcji w postaci 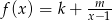 , gdzie
, gdzie 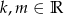 .
. - Wyznacz wszystkie wartosci
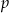 , dla których w przedziale
, dla których w przedziale 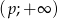 funkcja jest malejąca.
funkcja jest malejąca.
Funkcja homograficzna 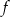 jest monotoniczna w przedziałach
jest monotoniczna w przedziałach 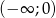 i
i 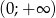 . Zbiór
. Zbiór 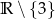 jest zbiorem wartości tej funkcji, a wartość 5 funkcja przyjmuje dla argumentu 3.
jest zbiorem wartości tej funkcji, a wartość 5 funkcja przyjmuje dla argumentu 3.
- Znajdź wzór funkcji
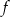 .
. - Wyznacz miejsce zerowe funkcji
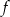 .
. - Wyznacz te argumenty, dla których funkcja
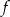 przyjmuje wartości większe od 1.
przyjmuje wartości większe od 1.
Uzasadnij, że funkcja 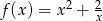 przyjmuje dla dodatnich argumentów wartości nie mniejsze niż 3.
przyjmuje dla dodatnich argumentów wartości nie mniejsze niż 3.
Wyznacz największą wartość funkcji 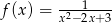 .
.
Wyznacz te wartości parametru 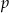 , dla których dziedziną funkcji
, dla których dziedziną funkcji 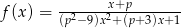 jest zbiór liczb rzeczywistych.
jest zbiór liczb rzeczywistych.
Na rysunku przedstawiony jest wykres funkcji 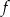 określonej wzorem
określonej wzorem 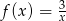 dla
dla 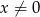 .
.
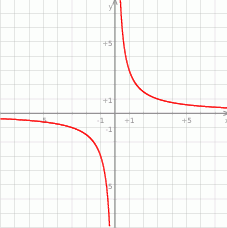
Wykres ten przesunięto o 2 jednostki w górę wzdłuż osi 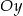 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 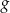 o wzorze
o wzorze 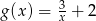 dla
dla 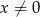 .
.
- Narysuj wykres funkcji
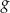 .
. - Oblicz największą wartość funkcji
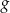 w przedziale
w przedziale 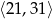 .
. - Podaj, o ile jednostek wzdłuż osi
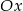 należy przesunąć wykres funkcji
należy przesunąć wykres funkcji 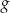 , aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
, aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
Wykres funkcji 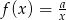 dla
dla 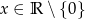 , gdzie
, gdzie 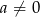 , przesunięto o wektor
, przesunięto o wektor ![→u = [− 3,2]](https://img.zadania.info/zad/2875082/HzadT3x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 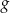 . Do wykresu funkcji
. Do wykresu funkcji 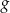 należy punkt
należy punkt 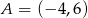 . Oblicz
. Oblicz  , następnie rozwiąż nierówność
, następnie rozwiąż nierówność 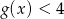 .
.
Dana jest funkcja 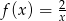 . Narysuj wykres i wyznacz przedziały monotoniczności funkcji
. Narysuj wykres i wyznacz przedziały monotoniczności funkcji 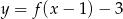 .
.
Sporządź wykres funkcji 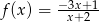 .
.

