Zestaw użytkownika nr 3177_7242
Logarytmy
Wykaż, że liczba 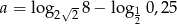 jest liczbą wymierną.
jest liczbą wymierną.
Oblicz 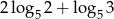 .
.
Wykaż, że liczba 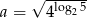 jest liczbą całkowitą.
jest liczbą całkowitą.
Oblicz 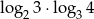 .
.
Wykaż, że 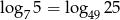 .
.
O liczbach  i
i 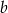 wiadomo, że
wiadomo, że 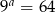 oraz
oraz 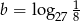 . Oblicz
. Oblicz 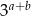 .
.
Uporządkuj rosnąco trzy liczby: 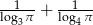 ,
, 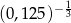 ,
, 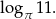 .
.
Liczby dodatnie 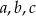 spełniają warunek:
spełniają warunek: 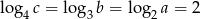 . Oblicz
. Oblicz 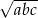 .
.
Oblicz 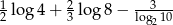 .
.
Oblicz 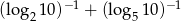 .
.
Wiadomo, że 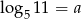 . Wykaż, że
. Wykaż, że 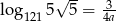 .
.
Oblicz wartość wyrażenia 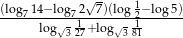 .
.
Wiedząc, że 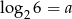 , wyznacz
, wyznacz 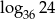 .
.
Oblicz 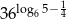 .
.
Nie korzystając z kalkulatora uzasadnij, że: 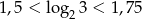 .
.
Udowodnij, że jeśli liczby dodatnie  i
i 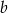 spełniają warunek
spełniają warunek 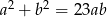 , to
, to 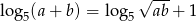 .
.
Ciąg geometryczny 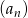 jest określony wzorem
jest określony wzorem 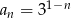 dla
dla 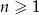 .
.
- Oblicz iloraz tego ciągu.
- Oblicz
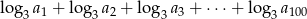 czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
Uporządkuj rosnąco liczby 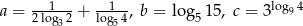 .
.
Widząc, że 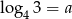 i
i 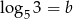 , wyznacz
, wyznacz 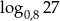 w zależności od
w zależności od  i
i 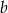 .
.
Wiadomo, że 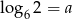 . Wyznacz
. Wyznacz 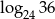 w zależności od
w zależności od  .
.
Wykaż, że dla liczb spełniających odpowiednie założenia (podaj te założenia) prawdziwy jest wzór: 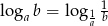 .
.
Wiedząc, że 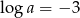 , a
, a 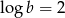 oblicz wartość wyrażenia
oblicz wartość wyrażenia 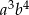 .
.
Wiedząc, że 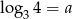 i
i 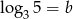 , wyznacz
, wyznacz 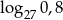 w zależności od
w zależności od  i
i 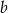 .
.
Udowodnij, że liczby 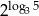 i
i 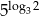 są równe.
są równe.
Wiedząc, że 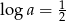 i
i 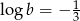 , oblicz
, oblicz 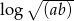 .
.
Korzystając ze wzoru
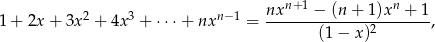
który jest prawdziwy dla dowolnej liczby naturalnej  i dowolnej liczby
i dowolnej liczby 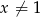 , wykaż, że
, wykaż, że
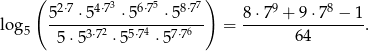
Nie używając kalkulatora, porównaj liczby: 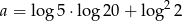 oraz
oraz 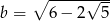 .
.
Wiedząc, że 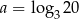 i
i 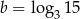 oblicz
oblicz 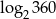 .
.
Oblicz wartość wyrażenia 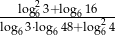 .
.

