Zestaw użytkownika nr 3272_9930
Zestaw użytkownika
nr 3272_9930
Tabela przedstawia pewne dane i ich liczebność
| Wartość danej | -4 | 2 | 4 | 7 | 20 |
| Liczebność | 7 | 2 | 3 | 6 | 2 |
- Oblicz średnią arytmetyczną tych danych.
- Podaj medianę.
- Oblicz odchylenie standardowe.
Uczniowie napisali pracę kontrolną. 30% uczniów otrzymało piątkę, 40% otrzymało czwórkę, 8 uczniów otrzymało trójkę, a pozostali ocenę dopuszczającą. Średnia ocen wynosiła 3,9. Ilu uczniów otrzymało piątkę?
Średnia arytmetyczna liczb: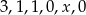 
jest równa 2. Oblicz 
.
Oblicz z dokładnością do 0,1 odchylenie standardowe następujących danych:
- -2; 0; 1; 4; 7; 14.
-
Wartość -3 -1 0 4 6 Liczebność 10 6 4 2 3
Uczeń otrzymał pięć ocen: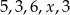 
. Średnia arytmetyczna tych ocen jest równa 4. Oblicz 
i medianę tych pięciu ocen.
Wyniki klasówki z matematyki, której średnia ocen była równa 3,5 przedstawiono w tabeli.
| Oceny | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba uczniów | 2 | 2 |  | 9 | 3 | 2 |
- Oblicz
. - Oblicz medianę danych.
Oblicz medianę danych: 0, 1, 3, 3, 1, 1, 2, 1.
Średnia wieku 15 mieszkańców pewnego bloku wynosi 33 lata. Gdy do wolnego mieszkania wprowadził się nowy mieszkaniec, średnia zwiększyła się o 1 rok. Ile lat ma nowy mieszkaniec?
Oblicz średnią arytmetyczną danych przedstawionych na poniższym diagramie częstości
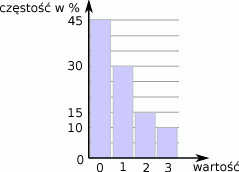
Mediana trzech liczb jest równa 4, a ich średnia arytmetyczna jest równa 5. Oblicz sumę największej i najmniejszej z tych liczb.
Średnia arytmetyczna liczb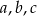 
jest równa 15. Oblicz średnią arytmetyczną liczb 
.
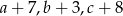Oblicz medianę następujących danych: 13,2; 15; 12,225; 14; 16,8; 42,7; 22,1; 31,4; 20,6; 18,4.
Oblicz medianę danych przedstawionych w postaci tabeli liczebności
| Wartość | 0 | 1 | 2 | 3 |
| Liczebność | 4 | 3 | 1 | 1 |
