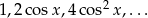Zestaw użytkownika nr 3850_8029
Zestaw użytkownika
nr 3850_8029
Pierwszy wyraz malejącego ciągu arytmetycznego 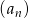 jest równy 3, a iloczyn wyrazów czwartego i piątego równy jest 15. Oblicz różnicę ciągu
jest równy 3, a iloczyn wyrazów czwartego i piątego równy jest 15. Oblicz różnicę ciągu  oraz sumę 14 jego początkowych wyrazów.
oraz sumę 14 jego początkowych wyrazów.
Podstawy czterech logarytmów liczby  tworzą ciąg geometryczny o ilorazie
tworzą ciąg geometryczny o ilorazie  . Wyznacz pierwszy z tych logarytmów jeśli jest on mniejszy od -1 oraz suma dwóch pierwszych logarytmów jest równa sumie dwóch pozostałych
. Wyznacz pierwszy z tych logarytmów jeśli jest on mniejszy od -1 oraz suma dwóch pierwszych logarytmów jest równa sumie dwóch pozostałych
Trzy początkowe wyrazy malejącego ciągu arytmetycznego są pierwiastkami wielomianu 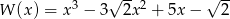 , a jednym z nich jest
, a jednym z nich jest 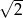 .
.
- Znajdź pierwszy wyraz tego ciągu.
- Oblicz sumę
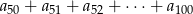 .
.
Podaj wzór na  -ty wyraz ciągu
-ty wyraz ciągu 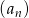 , jeżeli
, jeżeli 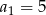 i
i 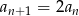 dla
dla 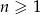 .
.
Iloczyn dziewięciu kolejnych początkowych wyrazów pewnego ciągu geometrycznego wynosi 512. Oblicz piąty wyraz tego ciągu.
Trzynasty wyraz ciągu geometrycznego jest równy 10. Oblicz wartość iloczynu dwudziestu pięciu początkowych wyrazów tego ciągu.
Udowodnij, że w ciągu geometrycznym 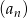 o wyrazach dodatnich iloczyn
o wyrazach dodatnich iloczyn 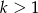 początkowych wyrazów ciągu jest równy
początkowych wyrazów ciągu jest równy 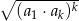 .
.
Wykaż, że jeżeli 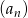 jest ciągiem geometrycznym, to ciąg
jest ciągiem geometrycznym, to ciąg 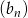 o wyrazie ogólnym określonym wzorem
o wyrazie ogólnym określonym wzorem 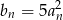 też jest ciągiem geometrycznym.
też jest ciągiem geometrycznym.
Oblicz sumę nieskończonego ciągu geometrycznego 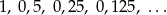
Wykaż, że suma szeregu geometrycznego zbieżnego jest ujemna wtedy i tylko wtedy, gdy jego pierwszy wyraz jest ujemny.
Wykaż, że jeżeli liczby 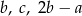 są kolejnymi wyrazami ciągu geometrycznego to liczby
są kolejnymi wyrazami ciągu geometrycznego to liczby 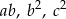 są kolejnymi wyrazami ciągu arytmetycznego.
są kolejnymi wyrazami ciągu arytmetycznego.
Dana jest funkcja określona wzorem 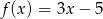 .
.
- Wyznacz ogólny wyraz ciągu
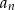 wiedząc, że:
wiedząc, że: 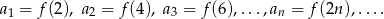
- Uzasadnij, że ciąg
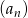 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym. - Oblicz sumę
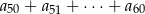 .
.
Ciąg 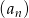 , gdzie
, gdzie 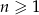 dany jest wzorem rekurencyjnym
dany jest wzorem rekurencyjnym
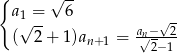
- Oblicz sumę 21 początkowych wyrazów tego ciągu.
- Wyznacz wszystkie liczby naturalne
 , dla których spełniona jest nierówność
, dla których spełniona jest nierówność 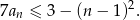
Wyznacz te wartości  , dla których istnieje suma nieskończonego ciągu geometrycznego
, dla których istnieje suma nieskończonego ciągu geometrycznego
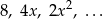 ,
,