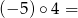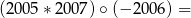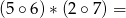Zestaw użytkownika nr 3933_3082

matura próbna rozszerzona z własności liczb

Zadanie 1
(5 pkt)

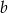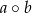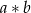Dla dowolnych liczb rzeczywistych a i b określamy liczby a ∘ b i a∗ b w następujący sposób:

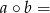  • a∘ b = liczba nie mniejsza spośród liczb a i b ,
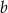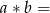  • a∗ b = liczba nie większa spośród liczb a i b.

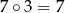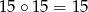Na przykład: 7 ∘3 = 7 , 15 ∘ 15 = 15 , 7∗ 3 = 3 , (− 6)∗ 4 = − 6 , (− 3) ∗(− 3) = −3 .
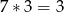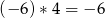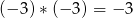Oblicz

  • (− 5)∘ 4 =
  • (2005 ∗ 2007) ∘(− 200 6) =
  • (5∘ 6) ∗(2 ∘ 7) =
Zadanie 2
(5 pkt)

Uzasadnij, że suma kwadratów dwóch kolejnych nieparzystych liczb całkowitych nie może być kwadratem liczby całkowitej.

Zadanie 3
(5 pkt)

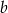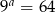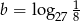O liczbach a i b wiadomo, że a 9 = 64 oraz 1 b = log 278 . Oblicz a+b 3 .

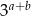Zadanie 4
(5 pkt)

Uprość wyrażenie

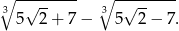
3∘ -√------- ∘3--√------ 5 2 + 7 − 5 2− 7.
Zadanie 5
(5 pkt)

Wiadomo, że liczba a jest rozwiązaniem równania 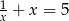1 x + x = 5 , gdzie 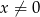x ⁄= 0 . Nie wyznaczając a , oblicz wartość wyrażenia 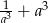1a3 + a3 .

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze