Zestaw użytkownika nr 4157_5877
Zestaw użytkownika
nr 4157_5877
Wyznacz zbiór wartości funkcji 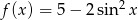 dla
dla 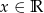 .
.
- Sprawdź, czy równość
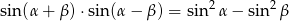
jest tożsamością trygonometryczną.
- Udowodnij, że jeżeli
 i
i 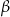 są dwoma kątami trójkąta i
są dwoma kątami trójkąta i 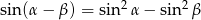 , to trójkąt ten jest trójkątem prostokątnym lub równoramiennym.
, to trójkąt ten jest trójkątem prostokątnym lub równoramiennym.
Wiedząc, że 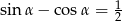 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 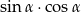 .
.
Wykaż, że wyrażenie 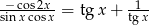 nie jest tożsamością.
nie jest tożsamością.
Posługując się wzorem 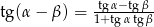 oblicz
oblicz 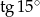 .
.
Sprawdź tożsamość: 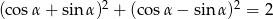 .
.
Wiedząc, że 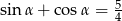 , oblicz
, oblicz 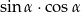 .
.
Oblicz 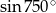 .
.
Dana jest funkcja 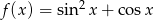 dla
dla 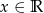 .
.
- Rozwiąż równanie
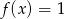 w przedziale
w przedziale 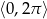 .
. - Wyznacz największą wartość funkcji
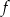 .
.
Kąt  jest ostry i
jest ostry i 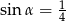 . Oblicz
. Oblicz 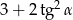 .
.
Wykaż, że 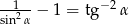 .
.
Kąt  jest kątem ostrym i
jest kątem ostrym i 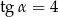 . Wyznacz sinus i cosinus tego kąta.
. Wyznacz sinus i cosinus tego kąta.
Uzasadnij, że jeżeli 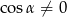 to prawdą jest, że
to prawdą jest, że 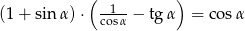 .
.
Wykaż, że wyrażenie 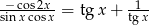 nie jest tożsamością.
nie jest tożsamością.
Sprawdź tożsamość: 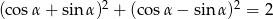 .
.
Sprawdź, czy prawdziwa jest następująca tożsamość 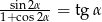 . Podaj konieczne założenia.
. Podaj konieczne założenia.
W trapezie równoramiennym przekątna ma długość 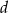 i tworzy z dłuższą podstawą kąt o mierze
i tworzy z dłuższą podstawą kąt o mierze  . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Romb o kącie ostrym 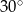 jest opisany na okręgu o promieniu 2. Oblicz pole tego rombu.
jest opisany na okręgu o promieniu 2. Oblicz pole tego rombu.
W trapezie kąty przy dłuższej podstawie to 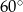 i
i 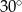 , a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.
, a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.
Pole rombu jest równe 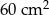 . Dłuższa przekątna rombu podzieliła kąt ostry rombu na takie dwa kąty o mierze
. Dłuższa przekątna rombu podzieliła kąt ostry rombu na takie dwa kąty o mierze  , że
, że 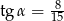 . Oblicz długość boku rombu.
. Oblicz długość boku rombu.
Dany jest trapez, w którym podstawy mają długość 4 cm i 10 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 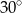 i
i 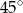 . Oblicz wysokość tego trapezu.
. Oblicz wysokość tego trapezu.
Z punktu 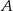 leżącego na okręgu o promieniu
leżącego na okręgu o promieniu 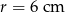 i środku
i środku 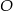 poprowadzono dwie równej długości cięciwy
poprowadzono dwie równej długości cięciwy 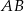 i
i 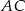 tworzące kąt
tworzące kąt 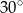 . Oblicz pole czworokąta
. Oblicz pole czworokąta 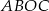 .
.
Długości boków równoległoboku 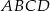 wynoszą 1 i
wynoszą 1 i 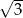 , a kąt przy wierzchołku
, a kąt przy wierzchołku 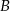 ma miarę
ma miarę 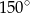 . Oblicz promień okręgu opisanego na trójkącie
. Oblicz promień okręgu opisanego na trójkącie 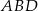 .
.
Dany jest trapez prostokątny (zobacz rysunek).
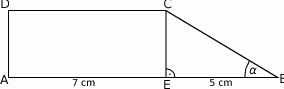
Wyznacz obwód tego trapezu, jeżeli miara kąta przy wierzchołku 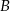 wynosi
wynosi 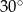 .
.

