Zestaw użytkownika nr 4514_9043

Zestaw użytkownika
nr 4514_9043

Zadanie 1

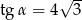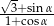Wiedząc, że α jest kątem ostrym oraz √ -- tg α = 4 3 oblicz wartość wyrażenia √ - --3+sinα 1+cosα .

Zadanie 2

Znajdź najmniejszą i największą wartość funkcji 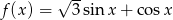√ -- f(x) = 3sinx + co sx w przedziale ⟨0 ;2π⟩ .

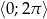Zadanie 3

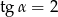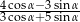Wiedząc, że α jest kątem ostrym i tgα = 2 , oblicz wartość wyrażenia 43-cocossαα−+-35ssininαα .

Zadanie 4

Wykaż, że wyrażenie 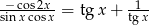−-cos2x- -1- sinxcosx = tg x + tgx nie jest tożsamością.

Zadanie 5

Wyznacz zbiór wartości funkcji: 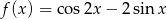f (x) = cos 2x− 2sin x , gdzie x ∈ R .

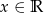Zadanie 6

Oblicz wartość wyrażenia 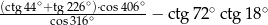(ctg44∘+tg226∘)⋅cos406∘ ∘ ∘ cos316∘ − ctg 72 ctg 18 .

Zadanie 7

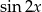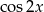Wyznacz sin 2x i cos2x jeśli wiadomo że 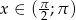π- x ∈ ( 2;π) i tgx = − 5 .

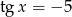Zadanie 8
  • Sprawdź, czy równość
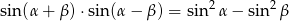
    sin (α+ β) ⋅sin (α− β) = sin2 α− sin 2β

    jest tożsamością trygonometryczną.

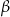  • Udowodnij, że jeżeli α i β są dwoma kątami trójkąta i 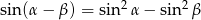sin (α− β) = sin2 α− sin 2β , to trójkąt ten jest trójkątem prostokątnym lub równoramiennym.
Zadanie 9

Wyznacz zbiór wartości funkcji 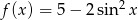2 f(x) = 5 − 2 sin x dla x ∈ R .

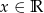Zadanie 10

Wyznacz najmniejszą wartość funkcji 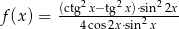(ctg2x−tg2x)⋅sin22x f(x) = ---4cos2x⋅sin2x---- .

Zadanie 11

Uzasadnij, że liczba 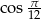π- cos 12 jest niewymierna.

Zadanie 12

Posługując się wzorem 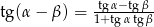-tgα−-tg-β- tg(α − β ) = 1+tgαtgβ oblicz ∘ tg 15 .

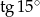Zadanie 13

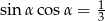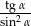Kąt α jest kątem ostrym. Wiedząc, że 1 sin α cosα = 3 , oblicz wartość wyrażenia tgα2-- sin α .

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze