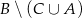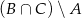Zestaw użytkownika nr 4886_3144
SprawdzianZ liczb15 Października 2011Czas pracy: 60 min.Suma punktów: 95
Suma dwóch liczb jest równa 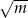 , a ich różnica jest równa
, a ich różnica jest równa 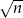 , gdzie
, gdzie 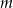 i
i  są dodatnimi liczbami całkowitymi. Wykaż, że iloczyn tych liczb jest liczbą wymierną.
są dodatnimi liczbami całkowitymi. Wykaż, że iloczyn tych liczb jest liczbą wymierną.
Niech 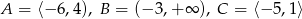 . Wyznacz zbiór
. Wyznacz zbiór 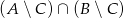 .
.
Oblicz 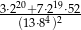 .
.
Suma dwóch liczb jest równa 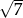 , a ich różnica
, a ich różnica 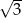 . Oblicz iloczyn tych liczb.
. Oblicz iloczyn tych liczb.
Stosując wzory skróconego mnożenia rozłóż na czynniki wyrażenie 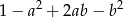 .
.
Wykaż, że suma kwadratów dwóch kolejnych liczb nieparzystych nie dzieli się przez 4.
Wykaż, że jeżeli 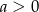 i
i 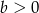 oraz
oraz 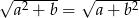 , to
, to 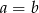 lub
lub 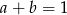 .
.
Wykaż, że liczba 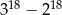 jest podzielna przez 19.
jest podzielna przez 19.
Oblicz 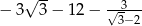 .
.
Uzasadnij, że jeżeli 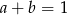 i
i 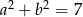 , to
, to 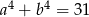 .
.
Wyrażenie 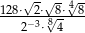 zapisz w postaci
zapisz w postaci 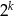 , gdzie
, gdzie 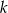 jest liczbą wymierną.
jest liczbą wymierną.
Wykaż, że jeżeli  jest liczbą nieparzystą to liczba
jest liczbą nieparzystą to liczba
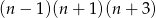
jest liczbą podzielną przez 48.
Usuń niewymierność z mianownika 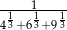 .
.
Oblicz 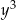 jeżeli
jeżeli 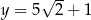 .
.
Oblicz 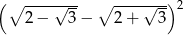 .
.
Oblicz ![[ ]1 8,25 − 0,5− 0,5 ⋅(2 −0,5 + 4− 0,25) 2](https://img.zadania.info/zad/7138971/HzadT0x.gif) .
.
Zapisz wyrażenie w prostszej postaci 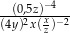 .
.
Uzasadnij, że jeżeli  jest liczbą całkowitą to liczba
jest liczbą całkowitą to liczba 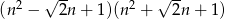 też jest liczbą całkowitą.
też jest liczbą całkowitą.
Dane są zbiory: 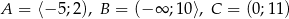 . Zapisz w postaci przedziału lub sumy przedziałów zbiory:
. Zapisz w postaci przedziału lub sumy przedziałów zbiory: