/Szkoła średnia/Zadania maturalne/Matura 2016/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 27 lutego 2016 Czas pracy: 180 minut
Zadania zamknięte
Suma szóstych potęg pierwiastków całkowitych równania 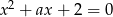 może być równa
może być równa
A) 65 B) 33 C) 2 D) 9
Ciąg 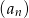 określony jest w następujący sposób
określony jest w następujący sposób 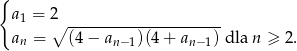 Setny wyraz ciągu
Setny wyraz ciągu 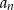 jest równy
jest równy
A) 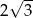 B) 2 C) 100 D)
B) 2 C) 100 D) 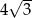
Która z poniższych funkcji nie ma minimum lokalnego ani maksimum lokalnego?
A) 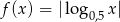 B)
B) 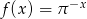 C)
C) 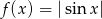 D)
D) 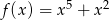
Równanie 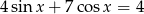
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma więcej niż dwa rozwiązania rzeczywiste.
Liczba 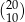 jest podzielna przez
jest podzielna przez
A) 5 B) 33 C) 221 D) 51
Zadania otwarte
Liczby 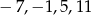 są miejscami zerowymi wielomianu czwartego stopnia
są miejscami zerowymi wielomianu czwartego stopnia 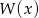 . Wykaż, że dla dowolnej liczby rzeczywistej
. Wykaż, że dla dowolnej liczby rzeczywistej  spełniona jest równość
spełniona jest równość 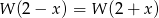 .
.
Oblicz granicę 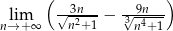 .
.
Oblicz pole trójkąta utworzonego przez prostą 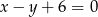 , oś
, oś 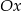 oraz styczną do wykresu funkcji
oraz styczną do wykresu funkcji 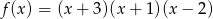 w punkcie o pierwszej współrzędnej
w punkcie o pierwszej współrzędnej 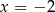 .
.
Niech 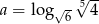 . Wykaż, że
. Wykaż, że 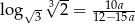 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 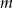 prawdziwa jest nierówność
prawdziwa jest nierówność 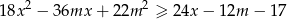 .
.
O zdarzeniach losowych 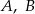 wiadomo, że:
wiadomo, że: 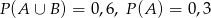 i
i 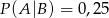 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 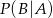 .
.
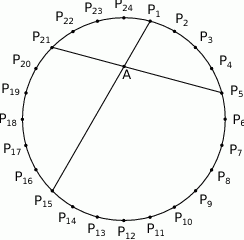
Punkty 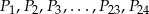 dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt
dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt 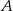 jest punktem przecięcia cięciw
jest punktem przecięcia cięciw 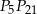 i
i 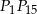 .
.
Udowodnij, że 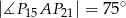 .
.
Dany jest trójkąt 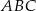 oraz punkt
oraz punkt 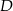 na jego boku
na jego boku 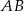 taki, że
taki, że 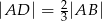 . Z wierzchołka
. Z wierzchołka 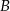 poprowadzono środkową
poprowadzono środkową 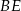 do boku
do boku 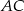 . Punkt
. Punkt 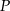 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 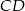 i
i 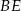 . Wykaż, że punkt
. Wykaż, że punkt 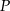 jest środkiem odcinka
jest środkiem odcinka 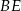 .
.
W trójkącie 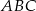 dane są:
dane są: 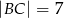 ,
, 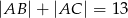 ,
, 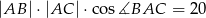 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
Rzucamy trzy razy monetą, a następnie rzucamy tyle razy kostką, ile orłów otrzymaliśmy w rzutach monetami. Oblicz prawdopodobieństwo tego, że suma oczek otrzymanych w rzutach kostką jest dwa razy większa od liczby orłów otrzymanych w rzutach monetą jeżeli wiadomo, że w rzutach monetą otrzymaliśmy przynajmniej jednego orła.
Współczynniki wielomianu 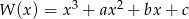 spełniają warunek:
spełniają warunek: 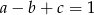 . Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki
. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki 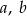 i
i  . Rozważ wszystkie możliwe przypadki.
. Rozważ wszystkie możliwe przypadki.
Rozpatrujemy wszystkie walce, których pole powierzchni całkowitej jest równe 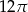 . Wyznacz wysokość tego spośród rozpatrywanych walców, którego objętość jest największa. Oblicz tę objętość.
. Wyznacz wysokość tego spośród rozpatrywanych walców, którego objętość jest największa. Oblicz tę objętość.

