Zestaw użytkownika nr 5120_1868
Zestaw użytkownika
nr 5120_1868
Z czterech ołowianych sześcianów o przekątnej długości 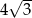 wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej graniastosłupa.
wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej graniastosłupa.
W graniastosłupie prawidłowym czworokątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu 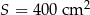 . Oblicz objętość i pole powierzchni całkowitej tej bryły .
. Oblicz objętość i pole powierzchni całkowitej tej bryły .
Oblicz długość przeciwprostokątnej trójkąta prostokątnego, wiedząc, że objętość brył powstałych z obrotu tego trójkąta wokół przyprostokątnych wynoszą odpowiednio 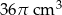 i
i 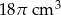 .
.
W sześcianie o krawędzi długości 2 połączono ze sobą środki trzech ścian mających wspólny wierzchołek. Sporządź odpowiedni rysunek i oblicz pole otrzymanego trójkąta.
Oblicz pole powierzchni i objętość sześcianu, którego przekątna ma długość 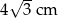 .
.
W ostrosłupie prawidłowym sześciokątnym pole przekroju płaszczyzną przechodzącą przez jego wysokość oraz przez dwie krawędzie boczne jest dwukrotnie większe od pola podstawy i wynosi 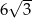 . Oblicz odległość spodka wysokości ostrosłupa od jego krawędzi bocznej.
. Oblicz odległość spodka wysokości ostrosłupa od jego krawędzi bocznej.
Podstawą graniastosłupa jest trapez równoramienny o podstawach długości 56cm i 40cm oraz wysokości 15cm. Wiedząc, że wysokość graniastosłupa jest równa 10cm, oblicz jego pole powierzchni całkowitej.
Graniastosłup prawidłowy trójkątny o krawędzi podstawy 4 cm i wysokości 10 cm przecięto płaszczyzną zawierającą wysokość podstawy i jedną z krawędzi bocznych. Jakie pole ma ten przekrój?
Oblicz wysokość graniastosłupa sześciokątnego prawidłowego, wiedząc, że krawędź podstawy ma długość 5cm, zaś najdłuższa przekątna graniastosłupa jest 4 razy dłuższa od najkrótszej przekątnej podstawy.
Podstawą ostrosłupa prawidłowego jest kwadrat o przekątnej 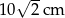 . Krawędź boczna ostrosłupa tworzy z podstawą kąt o mierze
. Krawędź boczna ostrosłupa tworzy z podstawą kąt o mierze 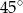 . Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa.
. Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa.
Długość promienia walca zmniejszono dziesięciokrotnie. Ile razy trzeba zwiększyć wysokość tego walca aby objętość się nie zmieniła?
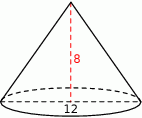
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie długości 12. Wysokość stożka jest równa 8. Oblicz pole powierzchni bocznej tego stożka.
Oblicz sinus kąta między przekątną sześcianu a jego płaszczyzną podstawy.
Oblicz objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy 2 dm i krawędzi bocznej 4 dm.
W ostrosłupie prawidłowym czworokątnym o objętości 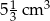 wysokość jest 2 razy dłuższa od krawędzi podstawy. Oblicz pole powierzchni tego ostrosłupa
wysokość jest 2 razy dłuższa od krawędzi podstawy. Oblicz pole powierzchni tego ostrosłupa
Oblicz objętość czworościanu foremnego o krawędzi  .
.
Wszystkie krawędzie ostrosłupa prawidłowego czworokątnego mają tę samą długość. Oblicz kąt nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Objętość stożka jest równa 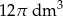 , a cosinus kąta
, a cosinus kąta  między wysokością, a tworzącą wynosi 0,8. Oblicz:
między wysokością, a tworzącą wynosi 0,8. Oblicz:
- pole powierzchni bocznej stożka;
- miarę kąta środkowego powierzchni bocznej stożka po rozwinięciu na płaszczyźnie.
Sześcian o krawędzi  przecięto płaszczyzną przechodzącą przez przekątną podstawy, która jest nachylona do płaszczyzny podstawy pod kątem
przecięto płaszczyzną przechodzącą przez przekątną podstawy, która jest nachylona do płaszczyzny podstawy pod kątem 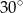 . Oblicz pole powstałego przekroju.
. Oblicz pole powstałego przekroju.
Podstawą prostopadłościanu jest kwadrat. Przekątna tego prostopadłościanu ma długość 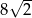 i jest nachylona do płaszczyzny podstawy pod kątem
i jest nachylona do płaszczyzny podstawy pod kątem 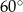 . Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek.
. Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek.
W prostopadłościanie pola trzech ścian o wspólnym wierzchołku są równe 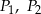 i
i 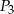 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Dany jest ostrosłup prawidłowy czworokątny o objętości 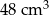 . Ściana boczna jest nachylona do podstawy pod takim kątem
. Ściana boczna jest nachylona do podstawy pod takim kątem  , że
, że 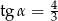 . Wyznacz pole powierzchni bocznej tego ostrosłupa.
. Wyznacz pole powierzchni bocznej tego ostrosłupa.
Oblicz objętość kuli wiedząc że jej pole powierzchni jest równe 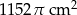 .
.
Suma długości wysokości i długości jednej krawędzi podstawy graniastosłupa prawidłowego czworokątnego jest równa 2. Jaką najmniejszą długość może mieć przekątna takiego graniastosłupa.
Oblicz wysokość i objętość ostrosłupa prawidłowego sześciokątnego o krawędzi podstawy 4 cm i krawędzi bocznej 10 cm.
Ołowianą kulę o średnicy 60 cm przetopiono na walce o wysokości i promieniu podstawy równych 2 cm. Ile takich walców otrzymano?
Wysokość prostopadłościanu o podstawie kwadratowej jest dwa razy dłuższa od krawędzi podstawy. Objętość prostopadłościanu jest równa 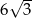 . Wyznacz pole powierzchni całkowitej tego prostopadłościanu.
. Wyznacz pole powierzchni całkowitej tego prostopadłościanu.
W graniastosłupie prawidłowym czworokątnym krawędź podstawy ma długość 5cm, a krawędź boczna ma długość 4cm. Przez wierzchołek górnej podstawy i przekątną dolnej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju. Rozpatrz 2 przypadki.
Graniastosłup prawidłowy czworokątny o krawędzi 4 cm i wysokości 3 cm przecięto płaszczyzną, która zawiera przekątne przeciwległych ścian bocznych. Jakie pole ma ten przekrój?
Kwadrat o boku długości 2 cm obraca się wokół swojej przekątnej. Oblicz objętość i pole powierzchni otrzymanej bryły.
Dany jest graniastosłup, którego podstawą jest równoległobok o polu 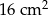 i kącie ostrym
i kącie ostrym 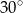 . Oblicz objętość graniastosłupa jeżeli pola jego ścian są równe
. Oblicz objętość graniastosłupa jeżeli pola jego ścian są równe 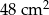 i
i 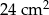 .
.
Promień i wysokość walca mają jednakową długość. Pole powierzchni bocznej wynosi 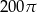 . Oblicz pole podstawy walca.
. Oblicz pole podstawy walca.

