Zestaw użytkownika nr 5433_7648
sprawdzian po klasie 1. rozszerzenie
Uzasadnij, że jeśli 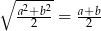 to
to 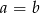 .
.
Wiadomo, że 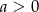 i
i 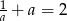 . Wykaż, że
. Wykaż, że 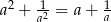 .
.
Wykaż, że jeżeli  jest liczbą nieparzystą to liczba
jest liczbą nieparzystą to liczba
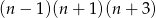
jest liczbą podzielną przez 48.
Wykaż, że kwadrat liczby całkowitej dającej z dzielenia przez 3 resztę 2, przy dzieleniu przez 3 daje resztę 1.
Wykaż, że dla dowolnych liczb rzeczywistych 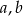 spełniona jest nierówność
spełniona jest nierówność
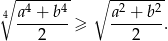
Wykaż, że prawdziwa jest nierówność 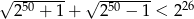 .
.
Rozwiąż nierówność 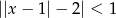 .
.
Rozwiąż nierówność 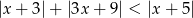 .
.
Trójkąty równoboczne 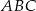 i
i 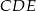 są położone tak, jak na poniższym rysunku. Wykaż, że
są położone tak, jak na poniższym rysunku. Wykaż, że 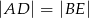 .
.
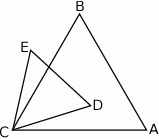
Na bokach trójkąta równobocznego zbudowano dwa kwadraty w sposób pokazany na rysunku.
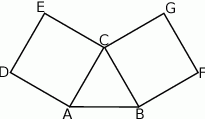
Wykaż, że punkty 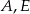 i
i 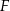 są wierzchołkami trójkąta prostokątnego.
są wierzchołkami trójkąta prostokątnego.
Wiedząc, że 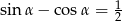 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 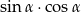 .
.
Wykaż, że nie istnieje kąt ostry  taki, że
taki, że 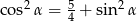 .
.
Za 4 lata Ula będzie miała dwa razy więcej lat niż miała 2 lata temu. Ile lat ma Ula?

