Zestaw użytkownika nr 5741_8141
Zestaw użytkownika
nr 5741_8141
Rozwiąż nierówność 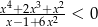 .
.
Określ liczbę pierwiastków równania 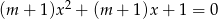 w zależności od wartości parametru
w zależności od wartości parametru 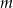 , a następnie naszkicuj wykres funkcji:
, a następnie naszkicuj wykres funkcji:

Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 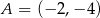 oraz
oraz 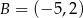 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 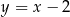 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Pierwszy wyraz nieskończonego ciągu geometrycznego 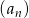 jest równy
jest równy 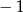 . Wyraz drugi, trzeci i czwarty spełniają warunek
. Wyraz drugi, trzeci i czwarty spełniają warunek 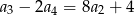 .
.
- Oblicz iloraz ciągu
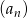 .
. - Określ, czy ciąg
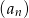 jest rosnący, czy malejący.
jest rosnący, czy malejący.
W trójkącie prostokątnym dany jest kąt ostry o mierze  i pole
i pole 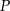 tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
Udowodnij, że jeśli
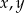 są liczbami rzeczywistymi, to
są liczbami rzeczywistymi, to 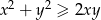 .
. 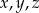 są liczbami rzeczywistymi takimi, że
są liczbami rzeczywistymi takimi, że 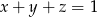 , to
, to 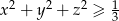 .
.
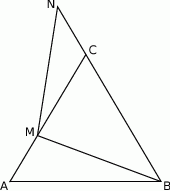
Trójkąt 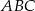 przedstawiony na poniższym rysunku jest równoboczny, a punkty
przedstawiony na poniższym rysunku jest równoboczny, a punkty 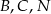 są współliniowe. Na boku
są współliniowe. Na boku 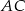 wybrano punkt
wybrano punkt 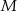 tak, że
tak, że 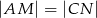 . Wykaż, że
. Wykaż, że 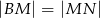 .
.
Podstawą ostrosłupa 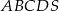 jest kwadrat
jest kwadrat 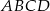 . Trójkąt równoramienny
. Trójkąt równoramienny 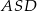 ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź
ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź 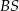 ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną
ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną 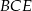 , gdzie
, gdzie 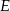 jest środkiem krawędzi
jest środkiem krawędzi 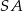 .
.
W urnie jest pewna liczba kul białych i jedna kula czarna. Losujemy jedną kulę z tej urny, zatrzymujemy ją, a następnie z pozostałych kul losujemy jedną kulę. Ile powinno być kul białych w urnie, aby prawdopodobieństwo wylosowania dwóch kul białych było równe 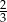 ?
?
Firma obuwnicza otrzymała zamówienie na wykonanie 720 par butów. Aby zrealizować zamówienie na czas, postanowiono wykonywać dziennie jednakową liczbę par butów. Po wykonaniu 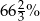 zamówienia usprawniono produkcję tak, że dzienna produkcja wzrosła o 4 pary, zaś zamówienie zrealizowano o 5 dni wcześniej. W ciągu ilu dni planowano wykonać zamówienie?
zamówienia usprawniono produkcję tak, że dzienna produkcja wzrosła o 4 pary, zaś zamówienie zrealizowano o 5 dni wcześniej. W ciągu ilu dni planowano wykonać zamówienie?

