Zadanie nr 5830326
Proste zawierające cięciwy 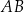 i
i 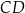 okręgu
okręgu  przecinają się w punkcie
przecinają się w punkcie 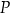 , który nie należy do okręgu
, który nie należy do okręgu  . Wykaż, że
. Wykaż, że
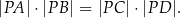
(Jest to tzw. twierdzenie o siecznych okręgu.)
Rozwiązanie
Jeżeli zaczniemy szkicować opisaną sytuację, to z pewnością zauważymy, że są dwie możliwe konfiguracje – punkt 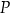 może leżeć wewnątrz lub na zewnątrz okręgu.
może leżeć wewnątrz lub na zewnątrz okręgu.

Zauważmy, że niezależnie od konfiguracji trójkąty 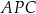 i
i  są podobne. Faktycznie, w obu sytuacjach jest jasne, że
są podobne. Faktycznie, w obu sytuacjach jest jasne, że
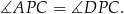
Ponadto, jeżeli punkt 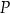 leży wewnątrz okręgu, to kąty
leży wewnątrz okręgu, to kąty 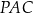 i
i 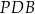 są równe jako kąty oparte na tym samym łuku. Jeżeli natomiast punkt
są równe jako kąty oparte na tym samym łuku. Jeżeli natomiast punkt 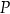 leży na zewnątrz okręgu, to czworokąt
leży na zewnątrz okręgu, to czworokąt 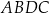 jest wpisany w okrąg i
jest wpisany w okrąg i
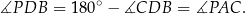
W takim razie w obu konfiguracjach trójkąty 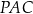 i
i 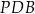 mają dwa równe kąty, więc są podobne. Stąd
mają dwa równe kąty, więc są podobne. Stąd
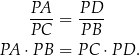
Jak łatwo uzasadnić, jeżeli punkt 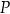 leży na zewnątrz okręgu, to iloczyn
leży na zewnątrz okręgu, to iloczyn 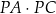 jest równy kwadratowi długości odcinka stycznej
jest równy kwadratowi długości odcinka stycznej  do okręgu poprowadzonej z punktu
do okręgu poprowadzonej z punktu 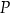 . Można użyć tej obserwacji jako alternatywnego dowodu równości
. Można użyć tej obserwacji jako alternatywnego dowodu równości

w przypadku, gdy punkt 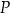 znajduje się na zewnątrz okręgu.
znajduje się na zewnątrz okręgu.

