/Szkoła średnia/Zadania maturalne/Matura 2023/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 18 marca 2023 Czas pracy: 180 minut
Oblicz granicę 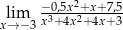
Oblicz, ile jest wszystkich liczb naturalnych sześciocyfrowych, w których zapisie występują dokładnie trzy cyfry nieparzyste.
Informacja do zadań 3.1 i 3.2
Dany jest ośmiokąt foremny  o boku długości 1.
o boku długości 1.
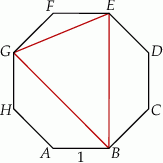
Udowodnij, że pole trójkąta  jest równe
jest równe 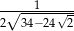 .
.
Niech 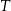 będzie środkiem odcinka
będzie środkiem odcinka 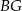 . Oblicz długość odcinka
. Oblicz długość odcinka 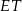 .
.
Dany jest nieskończony ciąg geometryczny 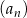 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 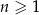 . Czwarty wyraz tego ciągu jest o
. Czwarty wyraz tego ciągu jest o  większy od drugiego wyrazu i jest mniejszy niż trzeci wyraz. Suma wszystkich wyrazów tego ciągu o numerach parzystych jest równa
większy od drugiego wyrazu i jest mniejszy niż trzeci wyraz. Suma wszystkich wyrazów tego ciągu o numerach parzystych jest równa 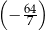 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości  , dla których spełniona jest nierówność
, dla których spełniona jest nierówność
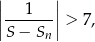
gdzie 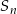 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 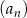 , a
, a 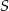 jest sumą wszystkich wszystkich wyrazów ciągu
jest sumą wszystkich wszystkich wyrazów ciągu 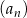 .
.
Wykaż, że dla każdej liczby rzeczywistej  mniejszej od
mniejszej od 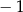 i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 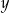 prawdziwa jest nierówność
prawdziwa jest nierówność 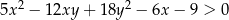 .
.
Prosta 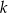 o równaniu
o równaniu 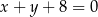 przecina parabolę o równaniu
przecina parabolę o równaniu 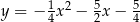 w punktach
w punktach 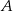 oraz
oraz 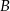 . Pierwsza współrzędna punktu
. Pierwsza współrzędna punktu 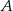 jest liczbą ujemną; pierwsza współrzędna punktu
jest liczbą ujemną; pierwsza współrzędna punktu 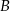 jest liczbą dodatnią. Prosta
jest liczbą dodatnią. Prosta 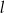 jest równoległa do prostej
jest równoległa do prostej 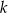 i styczna do danej paraboli w punkcie
i styczna do danej paraboli w punkcie 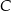 . Oblicz odległość punktu
. Oblicz odległość punktu 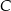 od prostej
od prostej 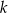 oraz pole trójkąta
oraz pole trójkąta 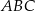 .
.
Rozwiąż równanie
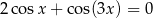
w zbiorze ![[− π ,π]](https://img.zadania.info/zes/0066873/HzesT37x.gif) .
.
W trójkącie 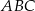 poprowadzono dwusieczne kątów przecinające boki
poprowadzono dwusieczne kątów przecinające boki 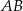 i
i 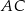 tego trójkąta w punktach – odpowiednio –
tego trójkąta w punktach – odpowiednio – 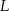 i
i 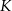 . Punkt
. Punkt 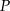 jest punktem przecięcia tych dwusiecznych. Długości boków trójkąta
jest punktem przecięcia tych dwusiecznych. Długości boków trójkąta 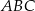 spełniają warunki:
spełniają warunki: 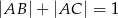 oraz
oraz
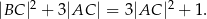
Udowodnij, że punkt 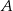 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 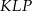 .
.
Wyznacz wszystkie wartości parametru 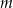 , dla których równanie
, dla których równanie
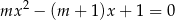
ma dwa różne rozwiązania rzeczywiste 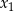 oraz
oraz 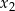 , spełniające warunek:
, spełniające warunek:
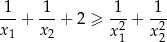
Podstawą ostrosłupa jest trójkąt prostokątny, w którym tangens jednego z kątów ostrych jest równy 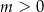 . Wszystkie krawędzie boczne ostrosłupa mają długość
. Wszystkie krawędzie boczne ostrosłupa mają długość 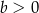 . Jakie powinno być pole podstawy ostrosłupa, aby jego objętość była największa? Oblicz tę największą objętość.
. Jakie powinno być pole podstawy ostrosłupa, aby jego objętość była największa? Oblicz tę największą objętość.
Wśród kilkuset studentów, którzy przystąpili do egzaminu z matematyki dokładnie jedna trzecia nie znała odpowiedzi na pierwsze pytanie. Egzaminator 10 razy wybrał z tej grupy studentów osobę i sprawdził czy zna odpowiedź na pierwsze pytanie (jedna osoba mogła zostać wybrana kilkukrotnie). Oblicz prawdopodobieństwo zdarzenia, że wśród tych wybranych 10 osób więcej niż połowa zna odpowiedź na pierwsze pytanie.

