Zestaw użytkownika nr 7646_1329
Zestaw użytkownika
nr 7646_1329
Wiedząc, że  jest kątem ostrym oraz
jest kątem ostrym oraz 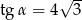 oblicz wartość wyrażenia
oblicz wartość wyrażenia 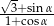 .
.
Wyznacz 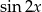 i
i 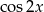 jeśli wiadomo że
jeśli wiadomo że 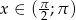 i
i 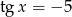 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 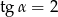 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 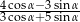 .
.
Wyznacz zbiór wartości funkcji 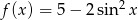 dla
dla 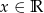 .
.
Uzasadnij, że jeżeli 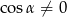 to prawdą jest, że
to prawdą jest, że 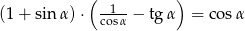 .
.
Dana jest funkcja 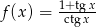 dla
dla 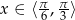 .
.
- Rozwiąż równanie
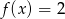 .
. - Wyznacz najmniejszą wartość funkcji
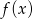 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 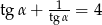 oblicz
oblicz 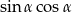 .
.
Wyznacz zbiór wartości funkcji: 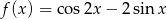 , gdzie
, gdzie 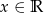 .
.
Kąt  jest kątem ostrym. Wiedząc, że
jest kątem ostrym. Wiedząc, że 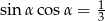 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 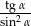 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 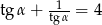 , oblicz
, oblicz 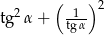 .
.
Wiedząc, że 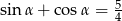 , oblicz
, oblicz 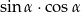 .
.
Dana jest funkcja 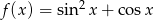 dla
dla 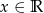 .
.
- Rozwiąż równanie
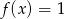 w przedziale
w przedziale 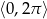 .
. - Wyznacz największą wartość funkcji
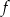 .
.
Kąta  jest ostry oraz
jest ostry oraz 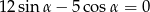 . Oblicz
. Oblicz 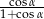 .
.
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to 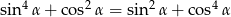 .
.
Kąt  jest taki, że
jest taki, że 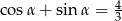 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 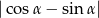 .
.
Rozwiąż równanie 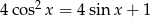 w przedziale
w przedziale 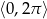 .
.
Rozwiąż równanie 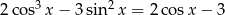 .
.
Rozwiąż równanie 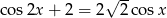 .
.
Dla jakich wartości parametru 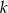 równanie
równanie 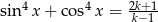 ma rozwiązanie?
ma rozwiązanie?
Rozwiąż równanie 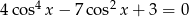 .
.
Rozwiąż równanie 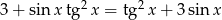 w przedziale
w przedziale 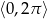 .
.
Rozwiąż równanie 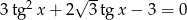 .
.
Wyznacz zbiór wartości parametru 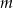 , dla których równanie:
, dla których równanie: 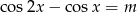 ma rozwiązania.
ma rozwiązania.
Rozwiąż równanie 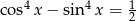 .
.
Rozwiąż nierówność 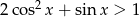 , gdzie
, gdzie 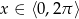 .
.

