/Szkoła średnia/Zadania maturalne/Matura 2018/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 17 marca 2018 Czas pracy: 180 minut
Zadania zamknięte
Liczba 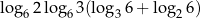 jest równa
jest równa
A) 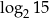 B)
B) 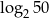 C) 1 D)
C) 1 D) 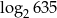
Rysunek przedstawia wykres funkcji 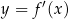 .
.
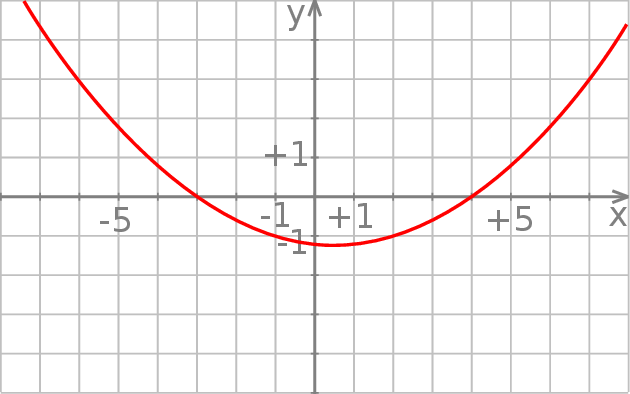
Wskaż wykres funkcji 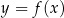 .
.
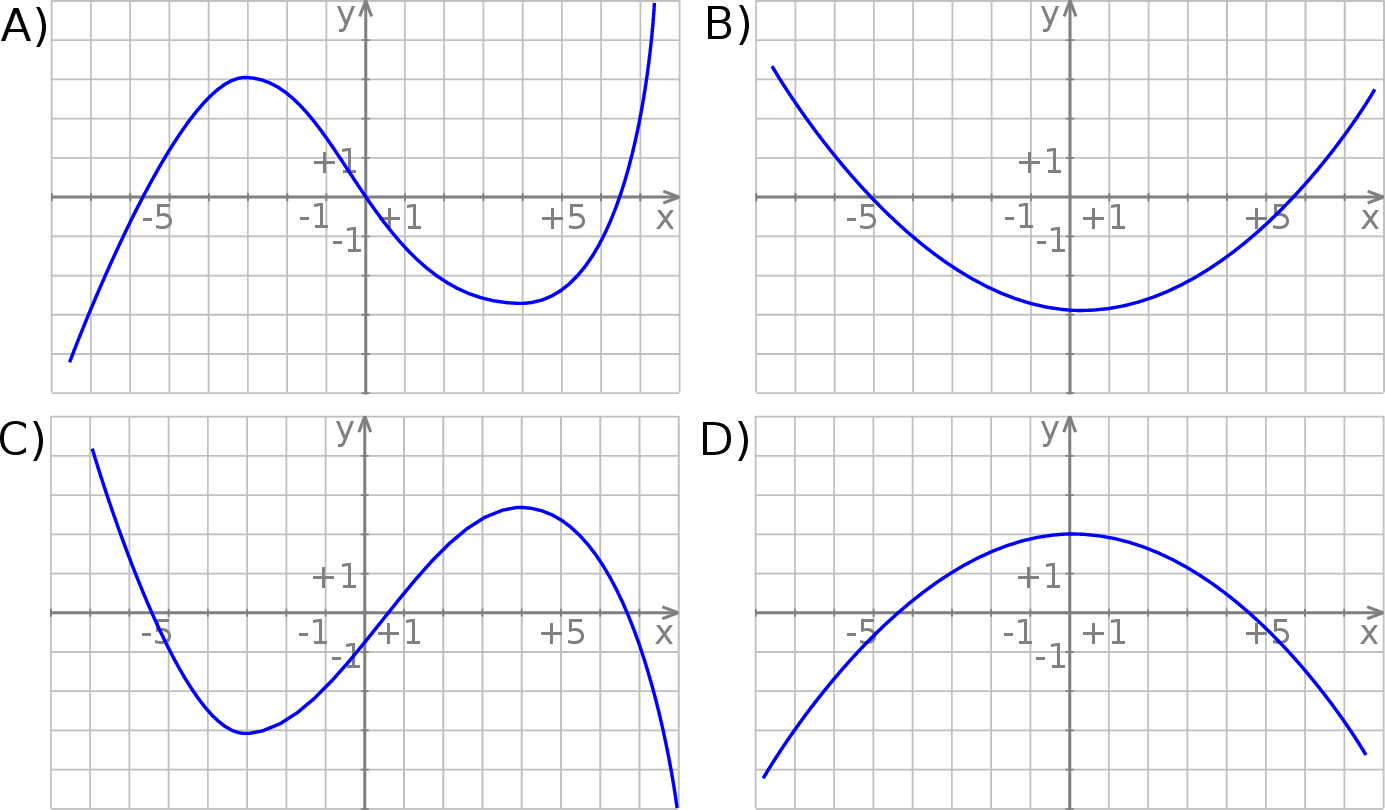
Nieskończony ciąg liczbowy jest określony wzorem 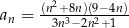 dla
dla 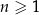 . Wtedy
. Wtedy
A) 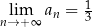 B)
B) 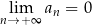 C)
C) 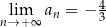 D)
D) 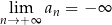
Okrąg o równaniu 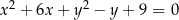 przesunięto o wektor
przesunięto o wektor ![[ ] 9,− 132](https://img.zadania.info/zes/0077827/HzesT15x.png) . Środek otrzymanego w ten sposób okręgu ma współrzędne
. Środek otrzymanego w ten sposób okręgu ma współrzędne
A) 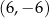 B)
B) 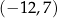 C)
C) 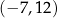 D)
D) 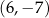
Dany jest nieskończony ciąg geometryczny, w którym suma wszystkich wyrazów jest 4 razy większa od sumy wszystkich wyrazów o numerach parzystych. Iloraz tego ciągu jest równy
A) 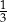 B)
B) 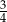 C) 1 D)
C) 1 D) 
Zadania otwarte
Na płaszczyźnie danych jest 100 punktów, z których żadne 3 nie leżą na jednej prostej. Ile jest różnych trójkątów o wierzchołkach w tych punktach?
Wyznacz wszystkie wartości parametru  , dla których prosta
, dla których prosta 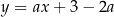 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 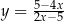 w punkcie o drugiej współrzędnej równej 3.
w punkcie o drugiej współrzędnej równej 3.
Przeciwległe boki czworokąta 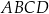 wpisanego w okrąg przecinają się w punktach
wpisanego w okrąg przecinają się w punktach 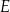 i
i 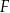 (zobacz rysunek), przy czym odcinek
(zobacz rysunek), przy czym odcinek 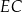 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 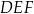 , a odcinek
, a odcinek 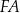 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 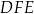 . Wykaż, że
. Wykaż, że 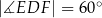 .
.

O zdarzeniach losowych 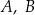 wiadomo, że:
wiadomo, że: 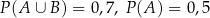 i
i 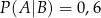 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 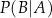 .
.
Przekątne trapezu równoramiennego 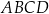 przecinają się w punkcie
przecinają się w punkcie 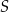 . Przekątna
. Przekątna 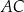 tworzy z dłuższą podstawą
tworzy z dłuższą podstawą 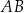 kąt
kąt  i z ramieniem
i z ramieniem 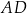 kąt
kąt 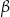 takie, że
takie, że 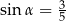 i
i 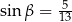 . Pole trapezu
. Pole trapezu 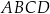 jest równe 448. Oblicz pole trójkąta
jest równe 448. Oblicz pole trójkąta 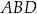 .
.
Trzy liczby całkowite tworzą ciąg geometryczny o ilorazie będącym ujemną liczbą całkowitą. Jeżeli najmniejszą z tych liczb zwiększymy o 9, to liczby te (w tej samej kolejności) są kolejnymi wyrazami ciągu arytmetycznego. Wyznacz te liczby.
Prosta 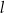 , na której leży punkt
, na której leży punkt 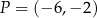 , tworzy z ujemnymi półosiami układu współrzędnych trójkąt prostokątny o polu równym 24. Wyznacz równanie prostej
, tworzy z ujemnymi półosiami układu współrzędnych trójkąt prostokątny o polu równym 24. Wyznacz równanie prostej 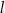 .
.
Rozwiąż równanie
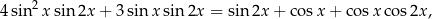
dla 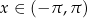 .
.
Podstawą ostrosłupa 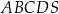 jest czworokąt
jest czworokąt 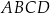 . Przekątna
. Przekątna 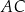 tego czworokąta ma długość
tego czworokąta ma długość 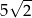 , a kąt
, a kąt 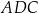 ma miarę
ma miarę 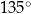 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 13. Oblicz sumę odległości spodka wysokości ostrosłupa od krawędzi bocznych
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 13. Oblicz sumę odległości spodka wysokości ostrosłupa od krawędzi bocznych 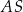 ,
, 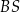 ,
, 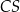 i
i 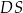 .
.
Maksymalny przedział, na którym funkcja 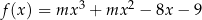 jest malejąca ma długość 2. Oblicz wartość parametru
jest malejąca ma długość 2. Oblicz wartość parametru 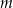 oraz wyznacz największą wartość funkcji na przedziale
oraz wyznacz największą wartość funkcji na przedziale 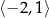 .
.
Wyznacz te punkty paraboli 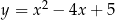 , które znajdują się najbliżej punktu
, które znajdują się najbliżej punktu 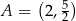 . Oblicz tę najmniejszą odległość.
. Oblicz tę najmniejszą odległość.

