Zadanie nr 7878316
W pudełku umieszczono  kul (
kul (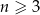 ) wśród których dokładnie 2 kule są czarne, a pozostałe kule są białe. Z tego pudełka losujemy jedną kulę i odkładamy ją na bok. Jeżeli wylosowana kula jest biała, to do pudełka wrzucamy kulę czarną, a gdy wylosowana kula jest czarna, to do pudełka wrzucamy kulę białą. Po przeprowadzonej w ten sposób zmianie zawartości prawdopodobieństwo wylosowania kuli białej z tego pudełka jest równe
) wśród których dokładnie 2 kule są czarne, a pozostałe kule są białe. Z tego pudełka losujemy jedną kulę i odkładamy ją na bok. Jeżeli wylosowana kula jest biała, to do pudełka wrzucamy kulę czarną, a gdy wylosowana kula jest czarna, to do pudełka wrzucamy kulę białą. Po przeprowadzonej w ten sposób zmianie zawartości prawdopodobieństwo wylosowania kuli białej z tego pudełka jest równe 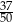 . Oblicz
. Oblicz  .
.
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

