Zestaw użytkownika nr 8126_8026
LogarytmyPowtórka przed maturą5 Lipca 2012Suma punktów: 105
Rozwiąż nierówność 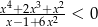 .
.
Wyznacz wszystkie wartości parametru 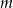 , dla których dziedziną funkcji
, dla których dziedziną funkcji
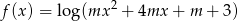
jest zbiór wszystkich liczb rzeczywistych.
Wyznacz zbiór wartości funkcji 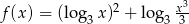 zdefiniowanej na przedziale
zdefiniowanej na przedziale 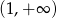 .
.
Wyznacz wszystkie wartości parametru 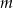 , dla których dziedziną funkcji
, dla których dziedziną funkcji
![2 2 f(x ) = log[(m + m − 6)x + (m − 2)x + 1]](https://img.zadania.info/zad/2939774/HzadT1x.gif)
jest zbiór wszystkich liczb rzeczywistych.
Wyznacz dziedzinę funkcji 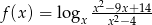 .
.
Określ dziedzinę funkcji 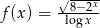 .
.
Wyznacz dziedzinę i najmniejszą wartość funkcji 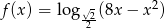 .
.
Wyznacz dziedzinę funkcji 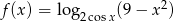 i zapisz ją w postaci sumy przedziałów liczbowych.
i zapisz ją w postaci sumy przedziałów liczbowych.
Wyznacz dziedzinę funkcji
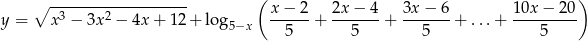
Wyznacz dziedzinę funkcji 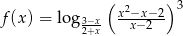
Dany jest wielomian 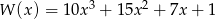 .
.
- Zapisz wielomian
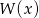 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych. - Określ dziedzinę funkcji
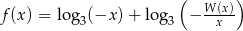 .
.
Wykaż, że liczba 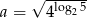 jest liczbą całkowitą.
jest liczbą całkowitą.
Uzasadnij, że liczba 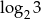 jest niewymierna.
jest niewymierna.
Wykaż, że liczba 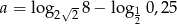 jest liczbą wymierną.
jest liczbą wymierną.
Korzystając ze wzoru
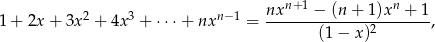
który jest prawdziwy dla dowolnej liczby naturalnej  i dowolnej liczby
i dowolnej liczby 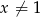 , wykaż, że
, wykaż, że
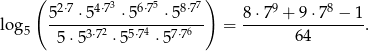
Ciąg geometryczny 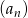 jest określony wzorem
jest określony wzorem 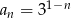 dla
dla 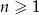 .
.
- Oblicz iloraz tego ciągu.
- Oblicz
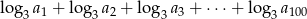 czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
O liczbach  i
i 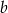 wiadomo, że
wiadomo, że 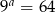 oraz
oraz 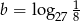 . Oblicz
. Oblicz 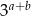 .
.
Wiedząc, że 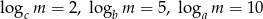 oblicz
oblicz 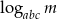 .
.
Wiadomo, że 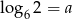 . Wyznacz
. Wyznacz 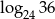 w zależności od
w zależności od  .
.
Wykaż, że dla liczb spełniających odpowiednie założenia (podaj te założenia) prawdziwy jest wzór: 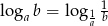 .
.
Wiedząc, że 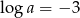 , a
, a 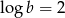 oblicz wartość wyrażenia
oblicz wartość wyrażenia 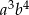 .
.

