Zestaw użytkownika nr 9358_8788
Zestaw użytkownika
nr 9358_8788
Dany jest ciąg arytmetyczny 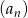 dla
dla 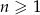 , w którym
, w którym 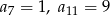 .
.
- Oblicz pierwszy wyraz
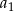 i różnicę
i różnicę  ciągu
ciągu 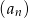 .
. - Sprawdź, czy ciąg
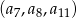 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 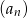 miała wartość najmniejszą.
miała wartość najmniejszą.
Liczby 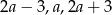 , w podanej kolejności, tworzą ciąg geometryczny. Wyznacz
, w podanej kolejności, tworzą ciąg geometryczny. Wyznacz  .
.
Wyznacz wszystkie wartości  , dla których ciąg
, dla których ciąg 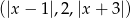 jest malejącym ciągiem arytmetycznym.
jest malejącym ciągiem arytmetycznym.
Cztery liczby tworzą ciąg geometryczny. Wyznacz te liczby wiedząc, że suma pierwszej i czwartej wynosi 36, a suma drugiej i trzeciej liczby wynosi 24.
Liczby 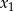 i
i 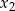 są pierwiastkami równania
są pierwiastkami równania 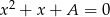 , a liczby
, a liczby 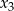 i
i 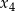 są pierwiastkami równania
są pierwiastkami równania 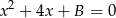 . Wiadomo, że ciąg
. Wiadomo, że ciąg 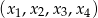 jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz
jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz 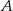 i
i 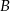 .
.
50 wyraz ciągu arytmetycznego 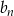 jest równy 5. Oblicz
jest równy 5. Oblicz 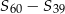 , gdzie
, gdzie 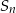 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 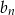 .
.
Jednym z pierwiastków trójmianu kwadratowego 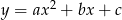 jest -0,2. Liczby
jest -0,2. Liczby 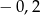 tworzą w podanej kolejności ciąg arytmetyczny, a ich suma wynosi 24. Oblicz drugi pierwiastek tego trójmianu.
tworzą w podanej kolejności ciąg arytmetyczny, a ich suma wynosi 24. Oblicz drugi pierwiastek tego trójmianu.
Liczby 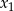 i
i 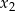 są różnymi miejscami zerowymi funkcji kwadratowej
są różnymi miejscami zerowymi funkcji kwadratowej 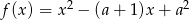 . Dla jakich
. Dla jakich 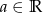 ciąg
ciąg 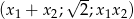 jest geometryczny?
jest geometryczny?
Cztery liczby tworzą ciąg geometryczny. Jeżeli od pierwszej z nich odejmiemy 2, od drugiej 3, od trzeciej 9, a od czwartej 25, to otrzymane różnice utworzą ciąg arytmetyczny. Znajdź te liczby.
Liczby  i
i 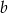 są pierwiastkami równania
są pierwiastkami równania 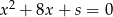 , a liczby
, a liczby  i
i 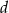 są pierwiastkami równania
są pierwiastkami równania 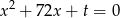 . Ciąg
. Ciąg 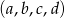 jest malejącym ciągiem geometrycznym. Oblicz
jest malejącym ciągiem geometrycznym. Oblicz  i
i 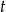 .
.
Trzy liczby tworzą ciąg geometryczny. Jeżeli drugą z nich zwiększymy o 8, to otrzymamy ciąg arytmetyczny. Jeżeli trzeci wyraz otrzymanego ciągu arytmetycznego zwiększymy o 64 to znów otrzymamy ciąg geometryczny. Wyznacz te liczby.
Oblicz wyrazy 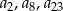 ciągu arytmetycznego jeśli
ciągu arytmetycznego jeśli 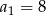 i
i 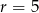 .
.
Dany jest ciąg 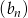 o wyrazie ogólnym
o wyrazie ogólnym 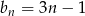 . Ile wyrazów ciągu
. Ile wyrazów ciągu 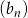 należy do przedziału
należy do przedziału 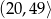 ?
?
Ciąg 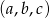 jest geometryczny, a ciągi
jest geometryczny, a ciągi 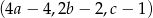 i
i 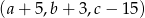 są arytmetyczne. Oblicz
są arytmetyczne. Oblicz 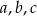 .
.
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 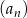 dla każdego
dla każdego 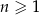 określona jest wzorem
określona jest wzorem 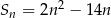 .
.
- Wykaż, że ciąg
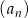 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym. - Wykaż, że jeżeli suma
 początkowych wyrazów ciągu dla każdego
początkowych wyrazów ciągu dla każdego 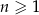 określona jest wzorem
określona jest wzorem 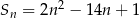 , to ciąg ten nie jest arytmetyczny.
, to ciąg ten nie jest arytmetyczny. - Znajdź takie trzy kolejne wyrazy ciągu
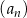 , aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.
, aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.
Ciąg 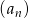 określony jest rekurencyjnie:
określony jest rekurencyjnie: 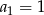 ,
, 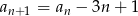 dla
dla 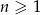 .
.
- Oblicz 4 wyraz ciągu
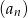 .
. - Zbadaj monotoniczność ciągu
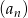 .
.
Wyznacz  tak, aby ciąg
tak, aby ciąg 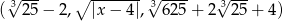 był ciągiem geometrycznym.
był ciągiem geometrycznym.
Ciąg 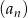 jest arytmetyczny oraz
jest arytmetyczny oraz 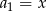 i
i 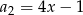 . Wiedząc, że
. Wiedząc, że 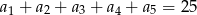 oblicz
oblicz  oraz sumę
oraz sumę 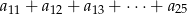 .
.
Oblicz iloczyn pierwszych 99 wyrazów ciągu geometrycznego 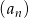 , w którym
, w którym 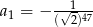 oraz
oraz 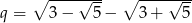 . Czy iloczyn ten jest liczbą wymierną?
. Czy iloczyn ten jest liczbą wymierną?
Znajdź wartość parametru 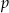 , dla której granica ciągu
, dla której granica ciągu 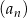 określonego wzorem
określonego wzorem
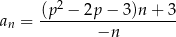
jest równa 4. Zbadaj monotoniczność ciągu 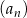 dla zanalezionej wartości
dla zanalezionej wartości 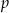 .
.

