Zestaw użytkownika nr 9463_8816

sprawdzian po 1. sem próbny 1

Zadanie 1

(4 pkt)

Uprość wyrażenie

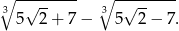
3∘ -√------- ∘3--√------ 5 2 + 7 − 5 2− 7.

Zadanie 2

(4 pkt)

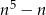Pokazać, że dla każdej liczby całkowitej liczba 5 n − n jest podzielna przez 30.

Zadanie 3

(4 pkt)

Boki trójkąta mają długości 4, 8 i 10.

Oblicz cosinus i tangens kąta leżącego naprzeciwko najkrótszego boku.
Oblicz długość środkowej poprowadzonej do najdłuższego boku.

Zadanie 4

(4 pkt)

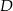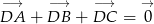Udowodnij, że jeżeli punkt jest środkiem ciężkości trójkąta, to −→ −→ −→ → DA + DB + DC = 0 .

Zadanie 5

(4 pkt)

Kwadrat o wierzchołkach 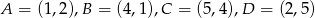A = (1,2),B = (4,1),C = (5,4),D = (2,5) przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach 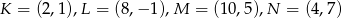K = (2,1 ),L = (8,− 1),M = (10,5),N = (4,7) . Wyznacz środek i skalę tej jednokładności.

Zadanie 6

(4 pkt)

Wyznacz równanie takiej prostej przechodzącej przez punkt 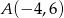A (− 4,6) , która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.

Zadanie 7

(4 pkt)

Oblicz wartość funkcji 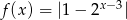x− 3 f(x) = |1 − 2 | dla argumentu

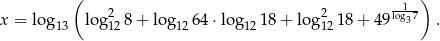
( --1-) x = log 13 log 2128+ lo g1264 ⋅log121 8+ log 21218 + 49log37 .

Zadanie 8

(4 pkt)

Wyznacz dziedzinę i najmniejszą wartość funkcji 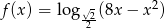√- 2 f(x) = log 22(8x − x ) .

Zadanie 9

(4 pkt)

Dla jakich wartości parametru 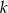równanie 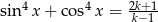4 4 2k+-1 sin x + co s x = k−1 ma rozwiązanie?

Zadanie 10

(4 pkt)

Określ liczbę rozwiązań układu równań 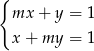{ mx + y = 1 x + my = 1 w zależności od wartości parametru 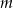. Dla tych wartości 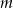, dla których istnieją rozwiązania, rozwiąż ten układ.

Zadanie 11

(5 pkt)

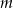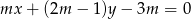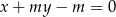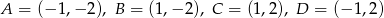Zbadaj dla jakich wartości parametru punkt przecięcia się prostych mx + (2m − 1)y − 3m = 0 i x + my − m = 0 należy do prostokąta o wierzchołkach A = (−1 ,−2 ), B = (1,− 2), C = (1,2), D = (− 1,2) ?

Zadanie 12

(5 pkt)

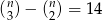Wyznacz liczbę , wiedząc że n n (3)− (2) = 14 .

Arkusz Wersja PDF