Zestaw użytkownika nr 9784_7637
Zestaw użytkownika
nr 9784_7637
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 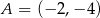 oraz
oraz 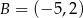 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 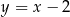 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma miarę 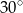 . Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
. Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
Rozwiąż równanie 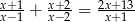 .
.
Pierwiastkami wielomianu 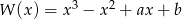 są tylko dwie liczby: 2 oraz (-3).
są tylko dwie liczby: 2 oraz (-3).
- Oblicz
 i
i 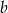 .
. - Zapisz wielomian w postaci czynników liniowych.
Na bokach 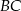 i
i 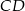 równoległoboku
równoległoboku 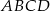 zbudowano kwadraty
zbudowano kwadraty 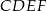 i
i 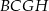 (zobacz rysunek).
(zobacz rysunek).
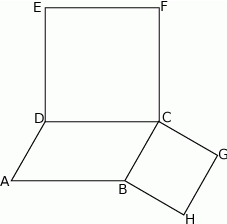
Udowodnij, że 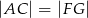 .
.
W trapezie równoramiennym przekątna ma długość 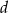 i tworzy z dłuższą podstawą kąt o mierze
i tworzy z dłuższą podstawą kąt o mierze  . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Rozwiąż równanie 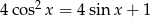 w przedziale
w przedziale 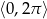 .
.
Danych jest osiem kul z numerami od 1 do 8, oraz dziesięć szuflad z numerami od 1 do 10. Rozmieszczamy w dowolny sposób kule w szufladach. Oblicz prawdopodobieństwa następujących zdarzeń:
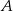 – wszystkie kule znajdą się w szufladach z numerami parzystymi.
– wszystkie kule znajdą się w szufladach z numerami parzystymi. 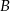 – dokładnie dwie szuflady pozostaną puste.
– dokładnie dwie szuflady pozostaną puste.
Miary kątów trójkąta są w stosunku 1:2:3. Obwód koła opisanego na tym trójkącie jest równy 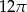 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
W trójkącie prostokątnym dany jest kąt ostry o mierze  i pole
i pole 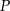 tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
Dany jest wielomian 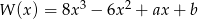 . Jednym pierwiastkiem wielomianu jest prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.
. Jednym pierwiastkiem wielomianu jest prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.
Znajdź  , dla którego liczby
, dla którego liczby 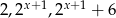 w podanej kolejności tworzą ciąg arytmetyczny.
w podanej kolejności tworzą ciąg arytmetyczny.
Rozwiąż nierówność
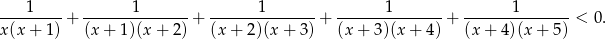
Dzienny dochód hurtowni akumulatorów wyraża się wzorem 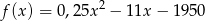 , gdzie
, gdzie  oznacza liczbę sprzedanych akumulatorów.
oznacza liczbę sprzedanych akumulatorów.
- Oblicz przy jakiej liczbie sprzedanych akumulatorów firma poniesie największą stratę. Oblicz wartość tej straty.
- Oblicz ile akumulatorów należy sprzedać, aby dzienny dochód wynosił 4985.
Rozwiąż równanie 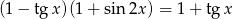 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 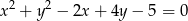 .
.
Mały Antek założył zeszyt, w którym każdego dnia zapisuje jedną liczbę. Pierwszą zapisaną przez niego liczbą było 112, a każdego następnego dnia zmniejsza wpisywaną liczbę o 7.
- Przez ile dni Antek wpisywał do zeszytu liczby, jeżeli wśród wpisanych liczb są liczby ujemne, a suma wszystkich liczb wynosi 805.
- Ile liczb dodatnich jest wpisanych do zeszytu?
Wysokość ostrosłupa prawidłowego czworokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość  .
.
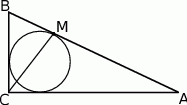
Dany jest trójkąt prostokątny 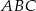 , w którym
, w którym 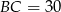 ,
, 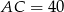 i
i 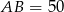 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 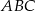 jest styczny do boku
jest styczny do boku 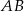 w punkcie
w punkcie 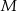 . Oblicz długość odcinka
. Oblicz długość odcinka 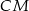 .
.
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia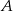 – na każdej kostce wypadła nieparzysta liczba oczek,
– na każdej kostce wypadła nieparzysta liczba oczek,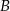 – suma wyrzuconych oczek jest nie mniejsza niż 8.
– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 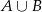 .
.
Wykres funkcji homograficznej 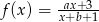 można otrzymać przesuwając wykres funkcji
można otrzymać przesuwając wykres funkcji 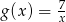 , a dziedzina funkcji
, a dziedzina funkcji 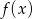 jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki
jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki  i
i 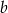 .
.
Dany jest wielomian 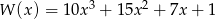 .
.
- Zapisz wielomian
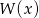 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych. - Określ dziedzinę funkcji
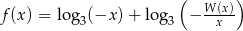 .
.
Odcinki 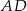 i
i 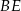 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 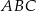 , a punkt
, a punkt 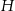 jest punktem ich przecięcia. Uzasadnij, że punkty
jest punktem ich przecięcia. Uzasadnij, że punkty 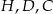 i
i 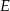 leżą na jednym okręgu.
leżą na jednym okręgu.
Wiedząc, że 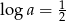 i
i 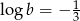 , oblicz
, oblicz 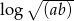 .
.
Uzasadnij, że jeżeli  jest liczbą całkowitą to liczba
jest liczbą całkowitą to liczba 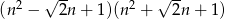 też jest liczbą całkowitą.
też jest liczbą całkowitą.

