Zadanie nr 8342123
Wszystkich liczb naturalnych trzycyfrowych o sumie cyfr równej 4 jest
A) 9 B) 8 C) 10 D) 11
Rozwiązanie
Zastanówmy się, ile niezerowych cyfr może mieć taka liczba? Jeżeli ma jedną niezerową cyfrę, to jest to liczba 400. Jeżeli ma dwie niezerowe cyfry, to mogą to być dwie dwójki lub 1 i 3. Łatwo wypisać wszystkie możliwe liczby tej postaci:
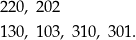
Jeżeli są trzy niezerowe cyfry, to muszą to być dwie jedynki i jedna dwójka. Są 3 takie liczby:
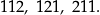
W sumie jest więc
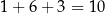
takich liczb.
Odpowiedź: C

