Zadanie nr 1203234
Wielomian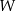 
określony wzorem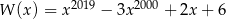 
A) jest podzielny przez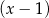 
i z dzielenia przez 
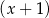daje resztę równą 6.
B) jest podzielny przez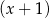 
i z dzielenia przez 
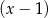daje resztę równą 6.
C) jest podzielny przez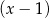 
i jest podzielny przez 
.
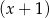D) nie jest podzielny ani przez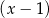 
, ani przez 
.
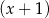Rozwiązanie
Reszta z dzielenia wielomianu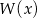 
przez dwumian 
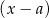to dokładnie 
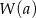(aby się o tym przekonać wystarczy podstawić 
w równości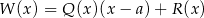 
).
W naszej sytuacji mamy więc
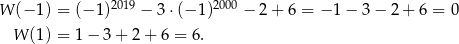
To oznacza, że wielomian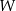 
dzieli się przez 
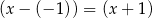i przy dzieleniu przez 
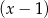daje resztę 6.
Odpowiedź: B
